QT1 P2 M 8

If k is a constant such that 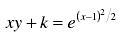satisfies the differential equation

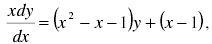, then k may be

(a) 1 (b) 0 (c) -1 (d) -2

ANS : 1

4 Answers

???????????????

The given eqn can be written as

log (xy+k) = (x-1)²/2

By differentiating the given expression we get

1/x + 1/y dy/dx = (x-1)(xy+k)

=> x dy/dx = (x² - x-1)y + k(x-1)

Comparing we get k =1

Thanks Govind & Avinav

see..log of xy+k...is not...log x+log y+log k
dis is wer u ve a mistake

EDITTED

√ √ || {} [] () → ~ ^ x x x → → ln log lg lim lim cos sin tan cot arcsin arccos arctan

∫ ∫ ∫ ∫ ∫ ∬ ∬ ∬ ∬ ∬ ∭ ∭ ∭ ∭ ∭ ⨌ ⨌ ⨌ ⨌ ⨌

∑ ∑ ∑ ∑ ∑ ∮ ∮ ∮ ∮ ∮ ∏ ∏ ∏ ∏ ∏ ∐ ∐ ∐ ∐ ∐

+ - × ÷ ± ∓ = ∪ ∩ ≠ ∼ ≈ ∅ ∀ ∃ ∈ ∋ ∝ ≤ ≥ ≃ ≅ ≡ < > ≪ ≫ ⊂ ∉ ⊃ ⊆ ⊇ ⇒ ⇐ ⇔ ⇒ ⇐ ⇔ ⇑ ⇓ ⇕ → ← ↔ → ← ↔ ↑ ↓ ↕ ↖ ↗ ↘ ↙ ↪ ↩ ⇀ ↼ ⇁ ↽

° ∂ ∞ α β γ δ θ λ μ ν ξ π ρ σ φ ω ε ƒ κ τ υ Γ Δ Λ Σ Π Ω