1help out
A uniform rope of mass m and length l is applied a force F on one end. What is the tension in the rope at a distance x from one end of the point of application of the force? (Assume uniform rope and that the cross section is 1 unit)
-
UP 0 DOWN 0 0 10
10 Answers
24λ=m/L
=>dm=λ.dx
Taking whole rope as system ,F=ma
Now take an element dx and distance s from where force is applied ..
m' x
=> m'=∫dm=∫λ.dx
0 0
=> m'=λx
Now see the forces on that element
=> F-T=m'a
=> F-T=(λx)(F/m)
=> T=F-mxF/Lm
=> T=F-Fx/L
=> T=F(1- x/L)
I know I made it a bit long...but that was done to elaborate the soln...I hope I am right
edited..missed a force..now its ok
24I took it to be horizontal...
I think u guys take it to be vertical
1eureka u hav neglected the force which is acting on the sytem....
the equation of motion should be
F-T=mxF/Lm
24oh yaa ..misse dit..actually I wasnt using pen or paper even..I was just typing..
1
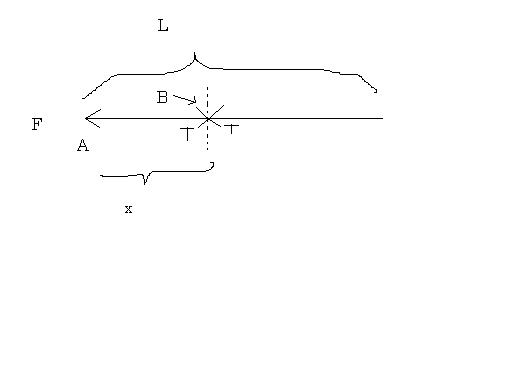
Taking the entire rope as one mass, F=ma; a=F/m;
Consider part AB.
F-T = Ma
Mass per unit length = m/L
Hence M=mx/L
T= F-Ma
= F-mxL.Fm
=F-FxL
The rope has been taken in a horizontal position (not a vertical one...I made a mistake in that). Cross-Secn. area has no use.
66That's right aveek.. you could have obtained that more simply if you considered the motion of the part of the rope leaving AB. Its mass is
mL(L-x)
And the acceleration F/m must be supplied by the tension. Hence,
T = mL(L-x) Fm = F(1 - xL)