1Isn't it pi/2?
The fundamental period of |sinx| + |cosx| is:
-
UP 0 DOWN 0 0 10
10 Answers
6@ ray ur right it will be pi/2.
can sumbody verify....
6
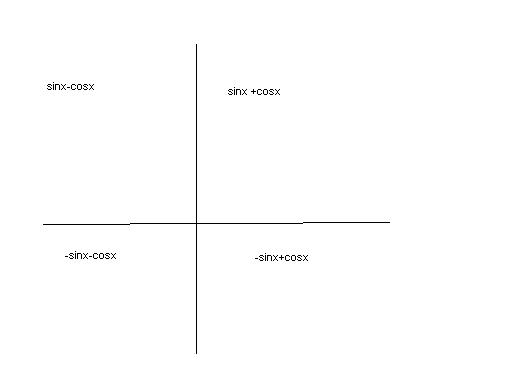
in first quad both sinx nd cos +ve
in second sinx-cosx
rest i have explained in graph.
now if u start from 1st quad ur searching for sinx+cosx
in 2nd quad u get cosx as -ve
so sinx- cosx becums sinx+cosx
thus u get pi/2.
u also get pi in thrid quad by applying the above logic
but since pi/2<pi
thus it is fundamental period....
6graph is simplest one
din u get my solution????
arrey itna bura bhi nahi hai.........:)
LOL
1just replace x by (x+ pi/2) :-
u get |sin(x+pi/2)|+|cos(x+pi/2)|
=|cos x|+|-sin x|=|sin x|+|cos x
thus period is pi/2
1u can also remember that...if the functions are complimentary, then just divide the h(that period which we get using the lcm) by 2
39Here we see that the actual fundamental periods of sin(x) and cos(x) are pi, separately. In combination however, it is an important rule for such functions that we check the period at T/2. Am posting the various points for periodicity of functions(if you already know them, refer the last point for the question) -:
1. If f(x) is periodic with period T, then f(ax + b) is periodic with period T|a|
2. A constant function is always periodic with no fundamental period.
3. If f(x) = f_{1}(x) \pm f_{2}(x) \pm... where f1(x), f2(x) etc are functions with periods T1, T2, etc, the function f(x) is periodic with a period which is the LCM of T1, T2, etc. If the LCM doesn't exist, neither does the period for f(x).
4. If f(x) = f_{1}(x) \pm f_{2}(x) \pm... are periodic with periods p1q1, etc then the function f(x) is periodic with period LCM(p1, p2...)HCF(q1, q2...). If either the LCM or HCF does not exist, neither does the period for f(x).
5. If f(x) is a periodic function and g(x) is non periodic,
A) gof(x) will always be periodic (may or may not be with the same period).
B) fog(x) will be periodic if and only if g(x) is a linear function of f(x) else it is non periodic.
6. If f(x) is periodic with period T, and g(x) may or may not be periodic but g(x) is an even function( f(x) and g(x) are in composition) then it is mandatory to check period at T/2.
7. If the functions in combination are complementary composite with period T, it is mandatory to check the period at T/2. (which is the case here)
cute cat, the period may not always be T/2. That's why it is mandatory to check.