this may help u http://en.wikipedia.org/wiki/Harmonic_series_(mathematics)#Divergence_of_the_harmonic_series
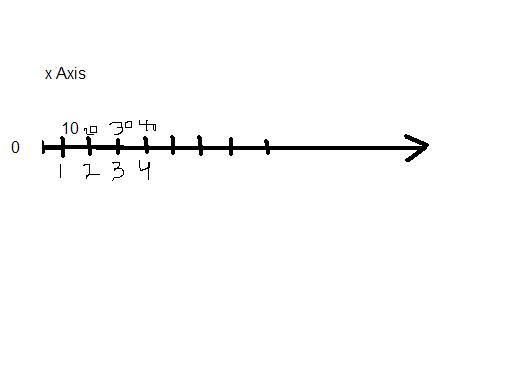
If on the x axis, charge 10 microcoulomb is kept at 1 unit, 20 microcoulomb at 2 units, 30 microcoulomb at 3 units...and so on till infinity.
What is the net electric field experienced by a positively charged particle kept at origin?
THE ANSWER IS NOT INFINITY.
When i begin solving this problem , i end up finding the sum of an infinite harmonic progression - whose sum as known is infinity.
Then, what other possible way there can be to tackle this question?
Can there be a substitution by a series? Such as log x or tan x?
14εn10-6{11+12+13....∞}
Any ideas?
-
UP 0 DOWN 0 0 5

5 Answers
no the problem lies not in finding the sum...i know its a diverging series.
But my question is how else to approach this problem for a finite answer.
I assume there may be a physical explanation for a finite answer...because mathematically it is infinite.
i have triple checked the question. I found this question in the old notebooks of my brother. No solution though. I only know it has a finite answer.
Will some of the fields cancel each other?
if the charges are alternating in sign then we can apply exapnsion of log and solve.