1062p/4p
p kaana??
solid angle kemiti kadhilu?
Two charges +q1 and and -q2 are placed at A and B respectively.A line of force emanate from +q1 at an angle α with AB. At what angle it will terminate at -q2?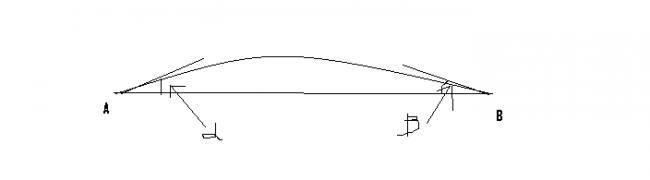
(a)sin-1[√(q1/q2)sin α/2]
(b)2sin-1[√(q1/q2)sin α/2]
(c)sin-1[√(q2/q1)sin α/2]
(d)2sin-1[√(q2/q1)sin α/2]
-
UP 0 DOWN 0 0 9
9 Answers
1Net flux from q1 enters q2....
q1E2p(1-cosA)4p = q2E2p(1-cosB)4p
=>B=2sin-1[√(q1/q2)sinA/2]
hence (b)
1net flux equate kali pa....
flux linkage due 2 q1 is over a solid angle of 2p4p(1-cosa)
1p=pi...actually i dont noe hw u all write so nicely...i dont get those!!!!
solid angle w(omega)=2pi(1-cosA2), where A is 2D angle in radians..
1arey in 4pi angle flux linkage is qE. so in w solid angle it will be w4pi....(unitary method)
