491)
E=q4πεor2 (I do not say this.. Guass does :P)
And if i have already not forgotten too many things,
Energy stored per unit volume of electrostatic field = ev = 12εoE2 (try proving yourself for any charge distribution)
total\;energy=\int e_vdV=\int_{R}^{2R}{\frac{1}{2}\epsilon _oE^2}.\pi r^2dr
Also: V = q4πεo.2R
Use these to reach a conclusion! [1]
49
Subhomoy Bakshi
·2011-06-17 04:48:18
2)
use same concept of energy stored per unit volume as we had done from R to 2R for 2R to ∞ and compare the total energy stored! [1]
49
Subhomoy Bakshi
·2011-06-17 04:50:42
I have a question for u Ashish:
Is my statement: V=q4πεo.2R right or wrong?
30Since, you have posted it, it can't be wrong. [3] Actually, I didn't get your question completely.
And the reason why I posted this question here was that my confusion was regarding the spheres. Since, the spheres are concentric, why can't they be considered as a capacitor?
49
Subhomoy Bakshi
·2011-06-17 07:38:17
Okay.. now I got your doubt!
So, @Ashish: I will give u a short self-evaluatory test here! The test tests how much of class stuff your head retains now!
I will upload an image.. that is the first hint why the system is not a capacitor...
next will be three hidden hints.. iff you cant get anything from hint 1 then and only then goto hint 2.. If you can figure out the answer from hint 1 then awesome! You can now check hint 2,3 and 4...
if not goto 2.. if u can figure out from 2 awesome...see 3,4
if not goto 3.. if u can figure out from 3 u r free to see 4 and have an awesome day ahead!
if not goto 4...and revise the class notes all over again..
Hint 1:
Given case:
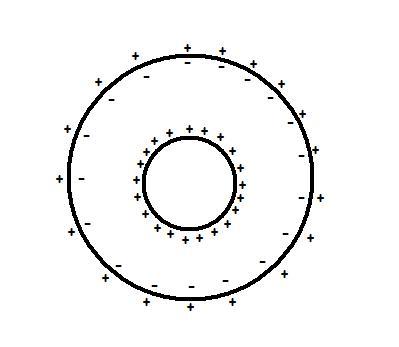
Rings any bell??
Hint 2: Draw field lines. any bells ring now??
Hint 3: Field inside and outside a capacitor.. Ding dong Ashish..:D
Hint 4: Capacitors class sheet 1.. :(
Answer: I wont give it.. you have to spend a day on it and post answer yourself.. if at doubt still I am there to help! [1]
49
Subhomoy Bakshi
·2011-06-17 07:39:44
Other users may feel free to post the answer in my chatbox but are heartily requested to refrain from posting their solutions and answers here in this post! [1]
Thanks..
All the best Ashish! :D
30
Ashish Kothari
·2011-06-17 08:29:06
This is the exact thing that came to my mind for your question "Is my statement: V=q
4πεo.2R right or wrong?" but I wasn't sure what you intended to ask?
Reason for it not being a spherical capacitor (I'm almost sure I wont be able to explain it) - While the charge distribution reminds me of electrical shielding, I feel charge distribution on the outer surface disturbs the idea of this being a capacitor. The charge distribution on the outer surface adds to the net potential inside which wouldn't be there in case of capacitor!
P.S. : I haven't yet seen the rest of the hints. But your verdict will decide whether I should, now, or noT! x
49
Subhomoy Bakshi
·2011-06-17 08:37:14
My hints were for the question:
Why is the setup not a capacitor?
u r right
Yes.. check the hints u might have nice entertainment!
V = q4πεo.2R wala question has nothing to do wid it..
*My question was: if q was the charge given to the inner sphere,
then V=
a) q4πεo.R
b) q4πεo.2R
c) q4πεo.R+q4πεo.2R
d) None of the above.
dont believe my answer it might be wrong for some reason! ;) give me some good reasoning.. dont even let a pinked post misguide you ;)
More questions:
What is the potential inside a spherical (2-shelled) capacitor?
30
Ashish Kothari
·2011-06-17 10:33:54
Okay just one question over here (btw I'm back after my bro finished watching X-Men [3]):
"*My question was: if q was the charge given to the inner sphere,then V=" : Are we considering the concentric sphere system?
49
Subhomoy Bakshi
·2011-06-17 10:45:48
yes that is w.r.t. the entire system..
V is as defined in the original question in #1..
q is the corresponding amount of charge given to the inner sphere!
rest is given in the thread itself! [1]
30
Ashish Kothari
·2011-06-17 10:55:13
Okay this is supremely interesting to engage in such a discussion. I hope I dont let you down in this one.
The potential V defined in the question is definitely V=q4πε°R.
Now,
assuming the capacitor having 2 concentric shells of radius R1 and R2 where R1<R2,
The potential is same everywhere inside the smaller shell and is equal to Q4πε°R+Q4πε°2R.
But the potential changes linearly once we move out of the smaller shell (thats what I feel cause even the field changes with distance!) [1]
30
Ashish Kothari
·2011-06-17 11:32:02
Okay one stupid mistake.. let the charge on the inner shell be -Q and the outer shell be +Q.
So potential anywhere inside the inner shell = -Q4πε°R1+Q4πε°R2
sab harbari mein garbari!
49
Subhomoy Bakshi
·2011-06-17 11:36:45
What for a disrance R2<r<R1
Whats the expression?
49
Subhomoy Bakshi
·2011-06-17 11:40:01
chalo theek hai..
As of now concentrate more on current electricity!
