The formula you gave is valid for a solenoid of infinite length.
An infinite solenoid, on addition of a few turns, remains an infinite solenoid.
the magnetic field inside a tightly wound long solenoid is b=μni .it suggests field does not depend on the length of solenoid .if we add more loops at the end of solenoid the field shud nt increase .explain qualitatively why extra added loop do not ve considerable effect on the field?
-
UP 0 DOWN 0 0 6

6 Answers
no actually the q ispractically adding more loops mean the intensity of magnetic field mst increase na (however the change cud be small ) bt theorotically its constant .why?
Arey, B=μ0ni is a completely theoretical concept------- hypothetical------ Don't mix it with practical things-------- you don't get infinite solenoids in practice.
If you consider a very long solenoid------ the magnetic field at abround the centre of the solenoid can be approximated by B=μ0ni
If you add loops, the field will increase but that will be a negligible increase------- so that the magnetic field at the centre can still be approximated by B=μ0ni
Please wait till tomorrow. I'll post the expression for the field inside a
"practical" (having finite length) solenoid. You'll see that as it's
length->∞ , B->μ0ni
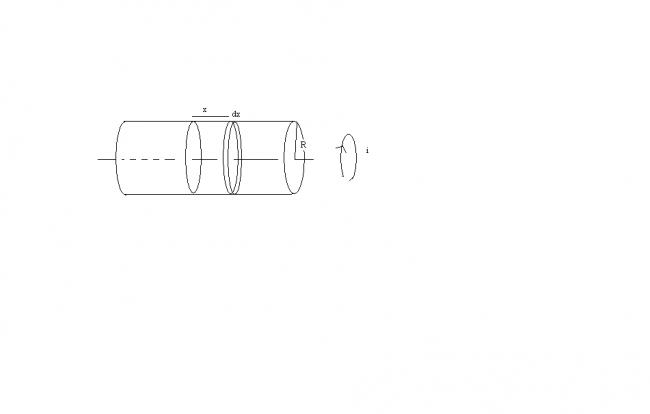
Here's the derivation for expression for the field in the middle of a solenoid of length L, number of turns n, current flowing "i" , and Radius R.
Field at centre due to an element dx (ring) at a distance x = dB =( μ0niR2dx)/2(R2+x2)3/2
So, net field = B = -L/2∫L/2 ( μ0niR2dx)/2(R2+x2)3/2
i,e. B= μ0niL /√(4R2+L2)
As you can see, with increase in L, B increases but the increase is negligible for large L.
And for L>>R , B≈ μ0ni
[I posted this, even though you've already understood, because I said I would do so.]