Thanks.. Got it now..
Q: Two fixed charges " +q " and " -q' " are shown as in the figure. A field line emerges from +q charge at an angle ' α '. Find the angle at which it terminates at the other charge.
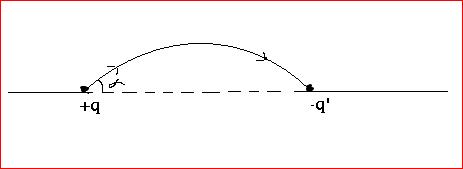
Note: | +q | ≠| -q' |
Please post Solution along with answer!
-
UP 0 DOWN 0 1 3

3 Answers
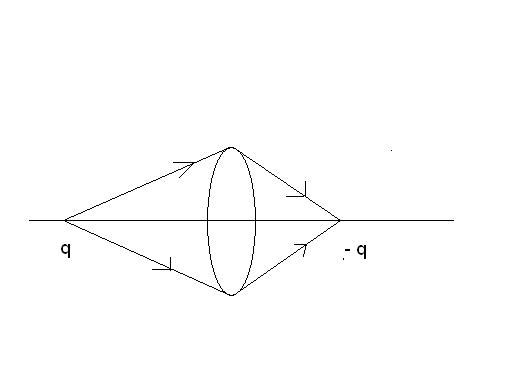
Draw a cone having a semi - vertical angle " α " that has its vertex at " q " , and let the same cone have its vertex at " - q ' " and have a semi - vertical angle " β " .
Obviously , if a field line emerges from " q " and enters " - q " , it must lie in the surface bounded by the cone , in other words , the number of field lines that are bounded by the cone on your left , must equal that by the cone of your right .
By Gauss ' s law , the number of field lines must equal the flux of the electric field through the cone .
Now , the flux of the electric field on the left side : q2 ε 0 ( 1 - cos α )
Similarly , on the right side , it is : q '2 ε 0 ( 1 - cos β )
Note that we must neglect the " - " sign as we are dealing with number of field lines .
Equaling these , we get the answer .