Well, A very unexpected result of posting this question herein. However, this was anyhow profitable for me that I managed to find my mistakes myself and and ultimately solve the problem.
So I care to post the solution here as any of you might come across it, So this will be helpful to you.
SOLUTION : :
We can think of problem from energy concept where if we find the potential energy of the charge at the apex of the cone, we can easily get the work done as ΔW = -ΔU.
Now to find the energy of the charge at the apex, we can visualize the cone as if made of various 'elemental' RINGS of varying radius. AS we good the formula for the potential energy due to a ring we can Integrate the expression to obtain the result.
That's all about Idea, Now,
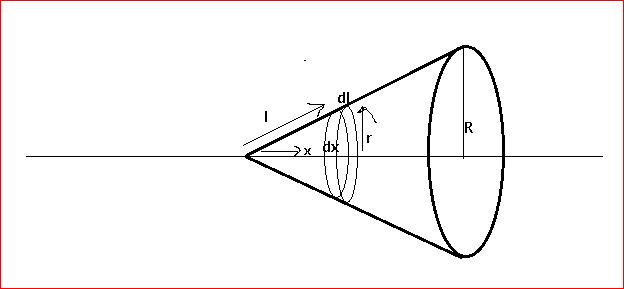
Taking any elemental Ring of radius ' r ' at a distance ' x ' from the apex of the cone which has a slanting length of ' l '.
Let thickness of the ring be ' ∂x ' and slanting thickness be ' ∂l '.
Now, Say σ (Charge density) = QπRL
Hence,
∂U = 14πε0 . q . ∂q√(r2+x2) ..... Potential Energy due to Ring and Charge
where, dq = σ . 2πr . ∂l
Replacing and Solving,
∂U = σ q r2ε0 . 1 l . ∂l
Replacing ' r ' by lR/L and Integrating the expression , On the right from 0 to L,
We Obtain,
ΔU = Qq2πε0L