1
Find the flux of the charge q through the upper cap of the cylinder....!!!.
(the charge q is kept on the bottom surface of the cylinder....)
assume the height to be h and the radius to be r
-
UP 0 DOWN 0 0 11
11 Answers
1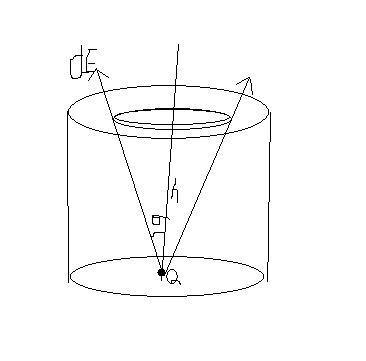
consider a strip of dx at a distance x.
the resultant field =2dEcosθ
now E=∫ 2dEcosθ
E= \int \frac{2KQ}{\sqrt{h^{2}+x^{2}}}\frac{h}{(h^{2}+x^{2})}
φ=E.dS
flux= \int \frac{2KQ}{\sqrt{h^{2}+x^{2}}}\frac{h}{(h^{2}+x^{2})} 2\pi xdx
now integrate and get the answer
23guyz pls see dis also
http://targetiit.com/iit-jee-forum/posts/polynomail-11969.html
sry for posting it here ..
1well flux through the cap is the answer dat i wanted....and that iota has written correctly.....
1arshad iota's answer is correct then the same u will get by integrating my integral
\int_{0}^{R}{\frac{4h\pi kqxdx}{\sqrt[3]{h^{2}+x^{2}}}}
take h2+x2=t 2xdx=dt dx=dt/2x
\int_{0}^{R}{\frac{2h\Pi kqdt}{t^{3/2}}}
integrating u will get
\frac{q}{2\epsilon }(1-\frac{h}{\sqrt{h^{2}+r^{2}}})
1sorry decoder i didnt look closely at urs......yes dats right too....but wat xyz has done is wrong...
1arshad evaluate my expression...
it also gives same.........btw i missed q in the expression