1HELP ME
19 Answers
62Potential is the work done to bring a unit charge from infinity to that point? (First is this definition correct...?)
If it is then what is the work done? Force x displacement.
This si all the theory you will need.
Then it is basically a questoin of realizing that we can make it simpler by some slight application here or there...
1but what about a point behind charge 'q' with distance from charge 'q' less than that of (1) and (2) ??
so in this case potential of charge behind 'q' has to be measured from the centre of the shell or from charge 'q' ?????? plz help there is a BIG trouble!!
1but what about a point behind charge 'q' ..with distance from chrge 'q' less than that of (1) and (2)??
...../.so in this case the potential of charge behind 'q' has to be mesurd from the centre of the shell or from charge q itself ..??
1the charge gets uniformly spread over the surfce of the conductor,and all points on spherical shell are at the same potential.
1
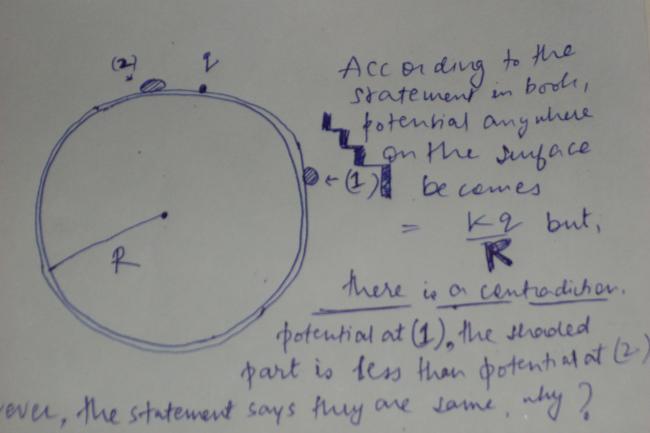hc verma pg-135 gauss law..-electric potential energy of a shell..the last statement in the 1st para reads:
"suppose at some instant charge 'q' is placed on the shell potential at the surface is kq/R"
how that is possible! ..,. that simply placing the charge 'q' at the surface makes potential independent of the distance from the charge 'q' itself?...and making it equal at all points on the surface?? plz help!!
1We know , Electric field E=kq/r2(outside sphere)r=R for surface...
-dV/dr=E so, ∫dv=-∫E.dr
∫dv=-qk∫(1/r2)d
r V=kq/r=(q/4πξ)R on surface
simple....
1
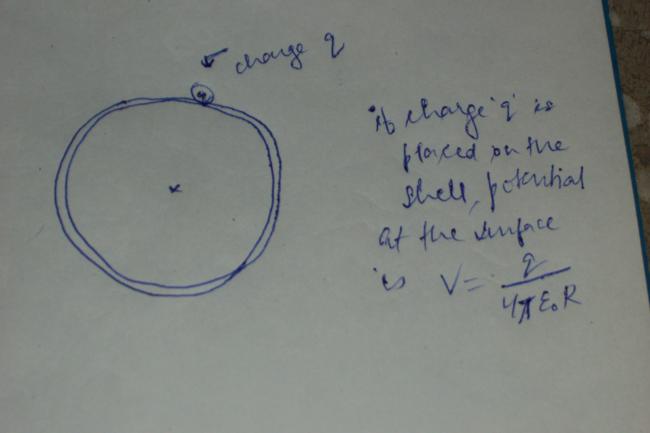
PLZ N E ONE HELP ME WITH THIS......WHAT IS THE POTENTIAL AT A POINT ADJACENT TO CHARge 'q'... is the ans q/4ΠεR.. ??
PLZ tell why the potential is so??i donno this qn at all!! it is so basic that is why it is makin me mad that i dont know the fundamentals like potential at the surface when a charge is placed on the shell??what is the anwer and why it is so??
1@ Prateek....This is very similar to finding the field & potential of hemisphere. 
1Thanks ,genius.
If you have time please try the thread "Electric field intensity"
,its still unsolved.
1Consider an elementary portion of the cone as a ring .
Let the radius of the base of the cone - R
Then , the charge carried by the elementary ring -
dq = σ ( 2 ΠR sin x ) R dx
So , the potential ,
dφ = dq4 Πε 0 R = σ R2 ε 0 sin x dx
Hence , the required potential ,
φ = σ R2 ε 0 ∫0Π/ 2 sin x dx = σ R2 ε 0
Here , σ = QΠR L
Hence , φ = Q2 Πε 0 L
Accodingly , the required work done = q φ = Q q2 Πε 0 L