24its easy........apply superposition.....
E+=Ï/3ε r1
E-=Ï/3ε r2
ER=E++E-
i hope remaining 2 steps u can do..............
(just use r1+r2=a)
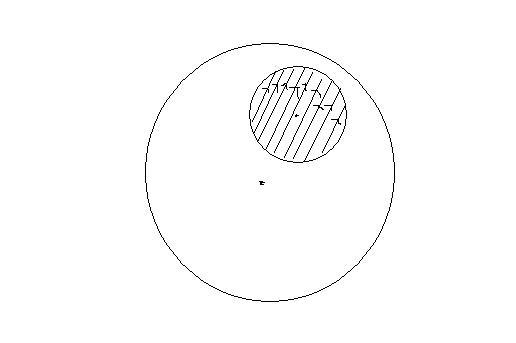
In a uniform sphere of charge density P (rho), a small cavity is created.
The center of the cavity is at a distance a from the center of the sphere. Taking center of the sphere as origin and vector a as unit vector along the line joining the center of cavity and origin find the electric field at a point inside the cavity.
-
UP 0 DOWN 0 0 5
5 Answers
24
62but eureka.. will it give the electric field at any aribitrary point if that point is not specified?
62you have to consider the radius vector of that point as r
and then take the electric field due to both these seperately... using guass's law.
Or am I still into my last night's sleep :)
33
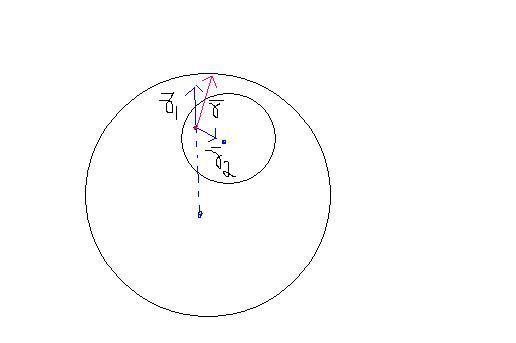
E+=(Ï/3ε) r1
E-=(Ï/3ε) r2 ....(Ï is not taken as negative as r2 is taken accordingly in opposite direction..)
ER=E++E-
(Ï/3ε)(r1+r2)
(Ï/3ε)r .. r is given unit vector joining two centers...
