hmmm thnxx bhaiiya
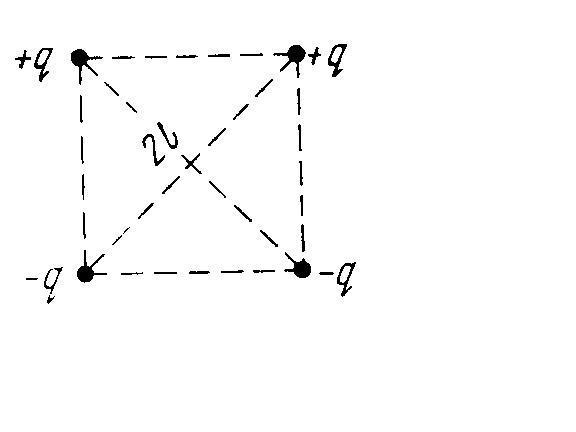
Point charges q and --q are located at the
vertices of a square with diagonals 2l as shown
. Find the magnitude of the electric
field strength at a point located symmetrically
with respect to the vertices of the square at a
distance x from its centre.
-
UP 0 DOWN 0 2 58

58 Answers
this seems to be a good learning experience for everyone. But in case u want the solutions to ur problems, as all of them aparently are from irodov, i would suggest u to look into this book- Abhay Kumar Singh, which has detailed solutions to all irodov problems. U could search for an e book of it, or look into the hard copy.
cheers!!!
THE DISTANCE x U R TALKING ABOUT IS PERPENDICULAR TO THE AREA OF SQUARE OR IN 2-DIMENSIONAL.
yes bhaiiya the doubtss r from irodov .....but the main thing is tht if have the solutions then i wud most probably be relying on 'em thtss why m not referin 'em......@katoch cant understand[1][7][7]
What is wrong in my solution ?
dQ=σ.dS
dQ=(ar)(2Ï€r dr)
∫dQ=2πa ∫0r r2dr
Q=2Ï€ar3/3
From Gauss Law
E.A=Q/ε
E(4πr2)=2πar3/3ε
E=ar/2ε
i have taken σ=aR means a.R ie aRcosθ.......is there i ve mistaken.....
u r right sanchit its dot product
now proceed without taking that cos component
hope u will get
σ = a r cos x , where x is the polar angle .
Polar angle means the angle made by the field vetor with the z - axis .
Now , the field is wrapped around the sphere in such a way that at the end points of a certain diameter , the field is zero and on either side of the diameter , the field is either negative or positive .
You can think of the sphere as superposition of 2 spheres , one having a +ve charge and another having a - ve charge , each being of same size .
So , the portion at the intersection of the 2 spheres has uniform electric field ,
E = Ï L / 3 ε 0 , where L is the vector separating the center of the two spheres .
Now , you have to find σ in terms of Ï and r only , otherewise you cannot express the result .
As the field is uniform , hence σ = Ï x ( the width of the intersected portion ) = Ï x d ( suppose )
From the figure , try to prove geometrically that , d = | L | cos x .
Hence , σ = a | R | cos x = Ï | L | cos x
Hence , a | R | = Ï | L |
Substituting the value , we get , E = - a R / 3 ε 0
The minus sign comes because the field vector is oppositely directed as compared to the z - axis .
P . S ------ Capital letters mean vetors . | K | means magnitude of vetor K . The bigger the " + " and " - " signs are , the bigger is the field there . The pink part of the picture is the distance " d " .


@gordo,
That view in #34 is not an acceptable one.
My suggestion: If you really want to learn, don't consult any solution book.
@kaymant sir, i agree with the point that you should try on your own. But what i said was, iff you don't get the answer to your question even after putting a lot of fight, you could refer to the book for the solution. I mean eventually, looking at the solution in the book, and solution of a person who solves the problem here is almost the same thing.
one more doubt easy one though
6) the electric feild vector is given by \vec{E}=a \sqrt{x} \hat{i}.FIND
a)the flux through a cube bounded by surfaces
x=l,x=2l,y=0,y=,l,z=0,z=l...
As electric field is in x-direction only, flux through surfaces perpendicular to x-axis exists.
For the surface at x=l, A (vec) = -l2 i
For the surface at x=2l, A (vec) = l2 i
=> flux thru surface at x=l is A (vec) . E (vec) = -l2 i.a√l i
= -al5/2
=> flux thru surface at x=2l is A (vec) . E (vec) = l2 i.a√2l i
= al5/2√2
So, net flux = al5/2(√2-1)
doubt no.
7)A point charge Q is moved along a circular path around another fixed point charge .the work done is zero
a)only if Q returns to its starting point
b)only if the two charges have same magnitude
c)only if the two charges have same magnitudes nd opposite signs.
d)in all cases
8) a + vely charged thin metal ring of radius R is fixed in the xy plane , with its center at the origin O. A - vely charged particle P is released from rest at point (0,0,z) where z>0.Then the motion of P is :
a)periodic ,for all values of z satisfying 0<z<∞.
b) simple harmonic,for all values of z satisfying 0<z≤R.
c)approximately simple harmonic provided z<<R.
d)such P crosses O nd continues to move along the - ve z axis towards z=-∞.
according to me answer shud be A nd C but answr given is A,C nd D
9) two large ,identical and parallel conducting plates have surfaces X nd Y ,facing each other .the charge per unit area on X is σ1 , nd on Y it is σ2.
a) σ1 =-σ2
b) σ1 =-σ2 only if charge is given to one plate only.
c) σ1 =σ2=0 if equal charges are given to both the plates.
d) σ1>σ2 if X is givenmore charge than Y.
one more is right
Ans 9) (a) , (c)
If two identical metal plates each having same surface area and charges 'q1' and 'q2' respectivey, are placed facing each other ..then charge distribution is as follows:-

Facing surfaces have equal and opposite nature of charges with magnitude half the difference of charge on different plates i.e is (q1-q2)2 in surface (2) and - (q1-q2)2 in surface (3).
hope u can see the image ma doubt here is tht how to find the equation of equipotential surface i got the electric field as E=2\sqrt{(a^2(x^2+y^2)+b^2z^2)}
7(d)
Work done by electric field zero,as change in PE =0 along eqipotential
circular path.v=kq*q/r=constant
arre haan it didnt strike ma mind thnxx ajoy !can u plzz try other also (10 nd 8)
φ = a(x2+y2)+bz2
\vec{E}=-[2ax\vec{i}+2ay\vec{j}+2bz\vec{k}]
hence \left| \vec{E}\right|=2\sqrt{a^{2}(x^{2}+y^{2})+b^{2}z^{2}}
shape of equipotential surface :
Put \vec{\rho }=x\vec{i}+y\vec{j} or {\rho }^{2}=x^{2}+y^{2}
then equipotential surface has the equation a{\rho }^{2}+bz^{2}=constant=\varphi
a) If a>0 , b>0 then φ>0 and the equation of the equipotential surface is \frac{\rho^{2} }{\varphi /a} +\frac{z^{2}}{\varphi /b} = 1
which is an ellipse in Ï and z co-ordinates .
In three dimensions the surface is an ellipsoid of revolution with semi-axis
\sqrt{\varphi /a},\sqrt{\varphi /a},\sqrt{\varphi /b}.
b) If a>0 , b<0 then φ can be ≥0. If φ > 0 then equation is
\frac{\rho^{2} }{\varphi /a} -\frac{z^{2}}{\varphi /\left| b\right|} = 1
this is a single cavity hyperboloid of revolution abt z-axis. If φ=0 then
a{\rho^{2} } -{z^{2}\left| b\right|} = 0
z=\pm\rho \sqrt{\frac{a}{\left|b \right|}}
is the equation of a right circular cone.
If φ < 0 then equation can be written as
\left|b \right|z^{2}-a\rho ^{2}=\left|\varphi \right|
\frac{z^{2}}{\left|\varphi \right|/\left|b \right|}-\frac{\rho ^{2}}{\left|\phi \right|/a} = 1
this is a two cavty hyperboloid of revolution abt z -axis
F=KQq.Z\R3 Take elemental charge ∂q on the ring having charge Q n then integrate sme as we do for finding the intensity only the cos component of force exists n on integration we get r ans as F=KQq.Z/(R2+Z2)3/2 n since z<<R ,r ans reduces 2 abv wrttn form
therefore (c)
thnxx mammay bhaiiya nd ahmand bhaiiya ........ve to think over it
@mammay bhaiiya thtss not in jee na

dq=\rho dx\\ F=\int_{-a}^{+a}\int_{b-a}^{b+a}\frac{1}{4\pi \epsilon_0}\frac{\rho^2 dx.dy}{(y-x)^2}\\ F=\frac{\rho ^2}{4\pi\epsilon_0}\ln\frac{x-(b+a)}{x-b+a}|_{-a}^{+a}\\ F=\frac{Q^2 K_e}{4a^2}\ln\frac{b^2}{b^2-4a^2}
