i have solved question asked by me...
plz.. solve question posted by abhishek
Four particles each having a charge q, are placed on the four vertices of a regular pentagon. The distance of each corner from the centre is a. Find the electric field at the centre of the pentagon..
ANS is q/(4πεa2)
plz give solution
-
UP 0 DOWN 0 0 17

17 Answers
Ok if u got that in ur attempt its fine.....
U should be satisfied by ur answer....... then thats OK.
i have taken b-c in vector form but i don't know how to write it in vector form
good work Abhishek...
:)
and Aman.. sorry for confusing u and wasting ur time !
One more interesting thing here E is independent of position of location of P in cavity.
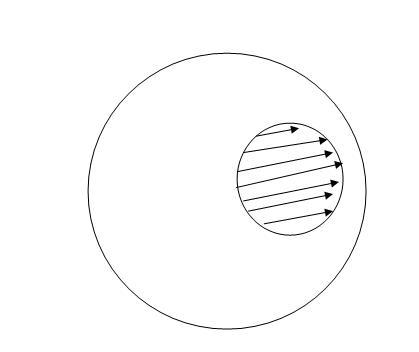
aslo direction is along line joining both center. and those arrows are showing uniform field.
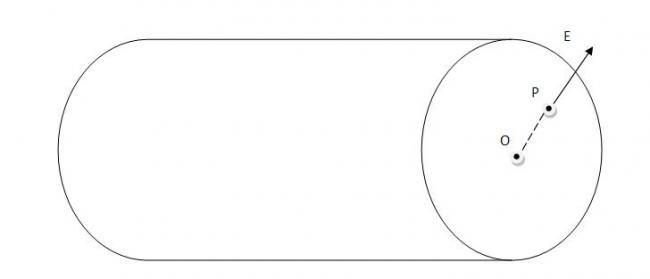
E at P is: OP Ï/2ε0
So in above question.........
E at P due to original cylinder...
E1=bÏ/2ε0
due to that cavity (assumed negative charge)
E2=c(-Ï)/2ε0
where c is position vector of P wrt center of cavity.
Net E =E1+E2=Ï/2ε0(b-c)
E=Ï/2ε0a
Ur answer is same magnitude wise but if u xpalin that (b-a)....
Wait how come you get b-a as distance of P frm center of cavity....
But got i think right answer.
U should use vectors to get directions as well....
take a gaussian surface (cylinder) passing through p with axis passing through centre of original cylinder
let height of cylinder be h
total charge inside gaussian cylinder= p π b2h
total flux = (p π b2h)/ε = E 2πb h
E= pb/2ε [electric field trough p due to original cylinder] .......(1)
take a gaussian surface (cylinder) passing through p with axis passing through centre of cavity
total charge inside gaussian cylinder= - p π(b-a )2h
total flux = (p π (b-a)2h)/ε = E 2π(b-a) h
E= - p(b-a)/2ε [electric field trough p due to - ve charge assumed in cavity] ........... (2)
adding 1 & 2
E= - pa/2ε
MAY BE I M WRONG
As i have said this in my earlier posts.. i think i will say this again.. i dont like posting full solutions bcos it is nothing other than spoonfeeding
so u need to take this whole set up as 2 things..
1) a cyllinder of radius R1 of charge density Ï
2) a cyllinder of radius R2 of charge density "-Ï"
now we know the distance from their center.. and also that this distance is less than the radius of both the cyllinders (so it is inside the cylliner)
Use superposition...
If u cant get it keep trying... u will get it :)
Post what u have tried... or where specifically u could not go further any longer...
aman this is simple...
think of this problem as aa fifth chargee of q placed on 5th corner along with a negative charge q on the 5th corner..
Note that the 5+q charges at the 5 corners will cancel themselves
so uwill remain with a single -q charge at the 5th corner.
hence the ANS is q/(4πεa2)
dear the first part's answer is rather simple (very very straight forward if u have understood it!)
Ok give me 5-10 mins.. i will post an image. that probably will make it a bit mroe clear to u!
i have understand the first part but answer still not coming
ok.. tell me this.. did u understand the first part that i solved?
if u did. then u should get this solution:
Try taking the central cyllinder as a overlap of +ve and -ve charge..
so u will have 2 uniform cyllinders of different radii...
Then take the solution from there!
no dear..
abhishek has given a very good hint there !!!
Try the addition and substraction of charges.. so that u get to some geometrical figure for which u knwo the potentials already!!!
using my method for solving ur problem..
answer to the question given by abhishek
pa/2e
e is epsilon
plz tel whether it is correct or not
Yes this method is gr8....
Arman U should also try...
Find the field at point P in cavity(cylindrical) in an infinite cylinder have uniform charge density Ï.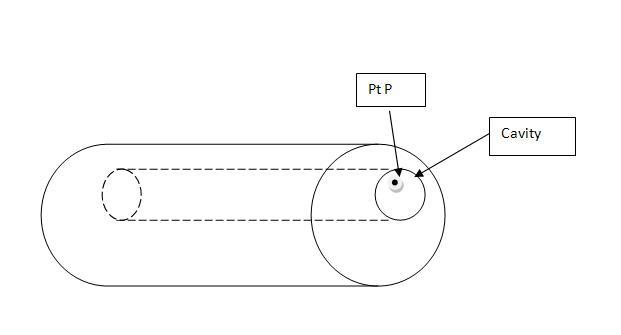
Take psition vector of center of cavity frm center of face of cylinder to be a and of point P frm center of face of Cylinder to be b
Try this method as told by Nishant only..........