Same logic as why velocity is tangential even though at every point motion is not (in circular motion)
If we find the magnetic field at a point due to a straight finite wire carrying current by Ampere's law, we get the same expression as for an infinite wire which is μ0I/2πr which is absurd bcoz for a finite wire it is given by (μ0I/4πr)*sin(θ1)+ sin(θ2))... So, where is the fallacy??? Or does ampere's law fail here???
-
UP 0 DOWN 0 0 20

20 Answers
but cud u plsss explain why is magnetic field different at different points even though symmetry is present???
and v use an imaginary loop in case of infinite wire n not cylinder.
also the line integral for finte wire will continue to be μ0I only but u cant use it to find B as B is curved for finite wire
uve typed wrongly
its actually (μ0I/4πr)*(sin(θ1)+ sin(θ2))
now for infinite wire θ1=θ2=90
sub ull get μ0I/2πr i donno what fallacy is there ?
The explanation goes this way......
It is right that the magnetic field is not constant, but not due to the reasons mentioned above. It is so coz in case of a finite wire, the magnetic field due to the elements of the circuit which is connected to the ends of the wire r also to be considered and that circuit may be non-symmetrical.
In case of an infinite wire too there is a circuit connected to its ends. But we say that the circuit too is at infinity and so it does not affect the magnetic field.
This reason may not seem to be perfect, but this is a standard reason and the most appropriate one.
bro why are u bringing infinite case in here again and again??????????
Infinite wire is enclosed in an imaginary cylinder.......this is purely diff case.......
try to read post #3 again........
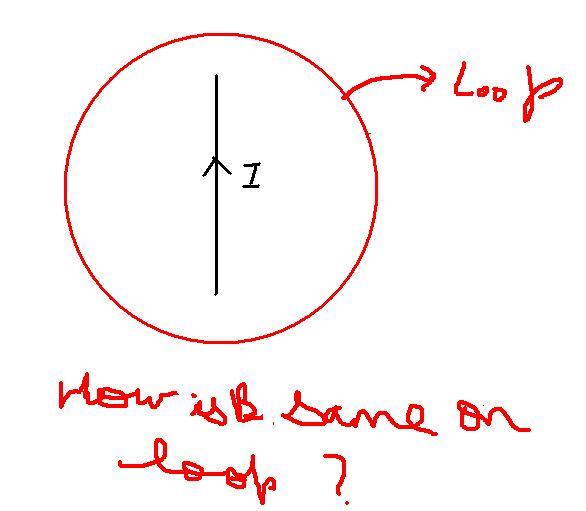
As this is a 3D figure, and the wire is passing through its centre and perpendicular to its plane, the wire cant distinguish between any points, rather any element of the loop due to symmetry principle......the same way we argue for an infinite wire.so the mag. field at all points must be the same
In short i just mean to say that all the symmetry principles hold good here as in the case of an infinite wire.
For all the points of the loop wont the magnetic field be constant??
Just consider the case of an infinite wire....we take the magnetic field at all the points of the loop to be constant,right.
The same way we can argue in this case too.
Only the difference of finite and infinite is present...rest all is same.
But why cant we use it here???
If We consider a point which is a an equal distance from both the ends,
all the above conditions r satisfied, isnt it? it is symmetrical and magnetic field is constant there as in the case of infinite wire.
It would be very wrong if we say that Ampere's Law fails...........
Its just that we are not using Amperes Law appropriately........
What does Ampere Circuital Law says.????
It says that draw an amperian loop in that region where magnetic field is constant and that current points(discrete or defined with some function)are distributed symmetricaly wrt loop.................
Magnetic field has to be constant about the loop so that closed path integral can be calculated[1] which is not the case here......[1]