Magnetics

\texttt{Let the current density be J} \\ \\ \mathrm{J=\frac{2I}{\pi a^2}}\\ \\

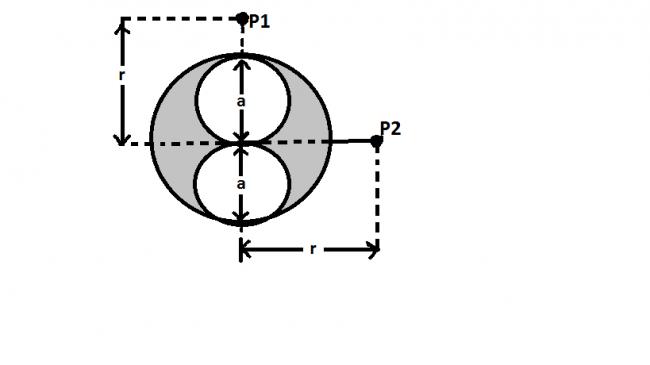
Now , consider this Cylinder

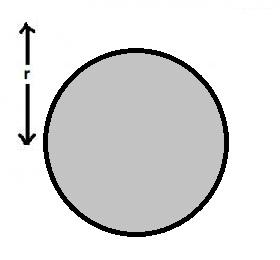
\texttt{Field at Point P1 due to this is } \\ \\ \mathrm{B_1=\frac{\mu_0 2I}{2\pi r}}

The direction is \mathrm{\hat{\theta}}

Now ,consider these two small cylinders one by one
But assume the current is going in the opposite direction
Due to the upper cylinder

\texttt{Field at Point P1 due to this is } \\ \\ \mathrm{B_2=\frac{\mu_0 I}{4\pi (r-\frac{a}{2})}}

Similarly ,consider the lower cylinder

\texttt{Field at Point P1 due to this is } \\ \\ \mathrm{B_3=\frac{\mu_0 2I}{4\pi (r+\frac{a}{2})}}

But B2 and B3 are in \mathrm{-\hat{\theta}}

So,net effet is
B1+B2+B3

B=\frac{\mu_0 I}{\pi}\left(\frac{1}{r}-\frac{1}{4}\left(\frac{1}{r-\frac{a}{2}}+\frac{1}{r+\frac{a}{2}} \right) \right)

Similarly , approach for 2nd one

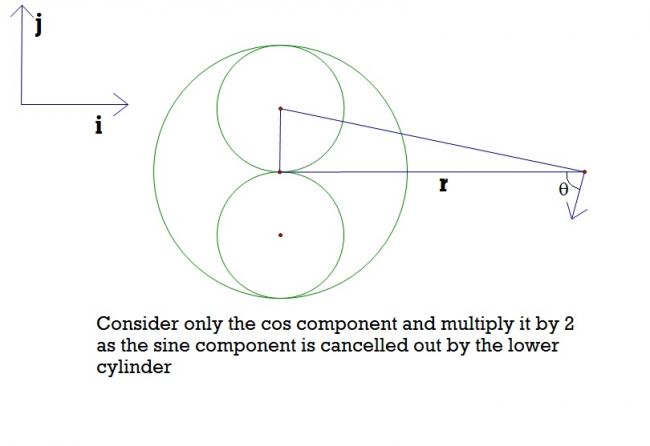
B=\frac{\mu_0 I}{4\pi\sqrt{r^2+\frac{a^2}{4}}}*\cos \theta \\ 2B=\frac{2 \mu_0 I}{4\pi\sqrt{r^2+\frac{a^2}{4}}}*\frac{a}{\sqrt{r^2+\frac{a^2}{4}}} (-\hat{i}) \\ \\ \\ 2B=\frac{2\mu_0Ia}{\pi\left(4r^2+a^2 \right)}(-\hat{i}) \\ \\ \texttt{B due yo biggest cylinder is } \\ \\ B'=\frac{\mu_0 I}{\pi r} (-\hat{j}) \\ \\ \bar{B}=B'-2B \\ \\ \bar{B}=\frac{\mu_0 I}{\pi}\left[\frac{2a}{4r^2+a^2}\hat{i}-\frac{1}{r}\hat{j} \right]

what are the answer given ?

its simple:
B=(mu*I)/(2*pi*R)
fo
r both the pts