496) Q:: A long, straight wire of radius r carries a current i and is placed horizontally in a uniform magnetic field pointing vertically upwards... The current is uniformly distributed ovr its cross sectional area... (a) At what points will the resultant magnetic field have maximum magnitude and what will be the maximum magnitude?
(b) What will be the minimum magnitude of the resultant magnetic field?
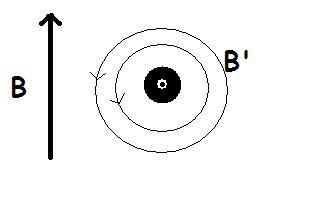
magnetic field will be maximum where direction of applied field is same as direction of produced field...
thus, it should be the rightmost point in the figure...
also the magnetic field will be maximum where the magnitude of the produced field will be maximum and from Ampere's circuital law it can just be found out that the produced field is maximum on the outer surface of the current conducting wire...
so the point is rightmost point of wire..on surface...
and the field is B+(Bproduced)max=B+μoi2πr in upward direction!!!
(b) there can be 2 answers for this!!
(i) When the value of maximum produced magnetic field, i.e. μoi2πr ≤ B the minimum magnitude will be when the produced field is maximum and the field is B-μoi2πr
(ii) but if
μoi2πr > B
then, minimum magnetic field is 0 and that is when produced magnetic field is equal to B and opposite in direction..i.e somewhere inside the wire...
Bproduced = μoπr'2πr2i2πr'=μoir'2πr2 where r'=distance of point from the axis of wire
min field for |Bproduced|=|B|
i.e. for r'=|B|.2πr2μoi...
hope doubt is cleared!!
1it is given tht i=1A
Bext=10-5T
r=0.02m
...................now u can use the formula ::B=μoI2πr[sinθ1+sinθ2]
since the given wire is an infinite one so put:: θ1=θ2=90
so, the expression become, B=μoI2πr
now the direction of B will be dot(outwards the plane of book/image) at P nd will be cross(inwards the plane) at Q.........so net Bnet=B+Bext.(put vector sign on them)
therefore ...u ll see tht Bnet at Q=0
nd at point p it ll get add up as they r in same direction pointing outwards(dot)
Bnet at P=2Bext κ
where is the unit vector along z axis
hope this ll help u!!!!!!!
1
sanchit
·2010-07-30 02:52:32
thtss the ques no. 5 i forgot to write tht
49
Subhomoy Bakshi
·2010-07-30 14:07:19
@Sanchit::.now u can use the formula ::B=μoI2πr[sinθ1+sinθ2]
since the given wire is an infinite one so put:: θ1=θ2=90°
so, the expression become, B=μoI2πr
Though i have not by-hearted the formulae, yet i can tell something is wrong in these lines!!
1
sanchit
·2010-07-31 02:21:56
ohh my mistake m really really srry for tht the correction is
now u can use the formula ::B=μoI4πr[sinθ1+sinθ2]
hope now tht is correct.........
