Charge is spayed onto a large non conducting belt above the left-handed roller as shown in the above figure. The belt carries the charge density s , as it moves with speed v b/w the rollers as shown. The charge is removed by a wiper at the right handed roller. Consider a point just above the surface of the moving belt. Find an expression for the magnitude of magnetic field at this point.
-
UP 0 DOWN 0 0 2
2 Answers
66We effectively have a surface current, the density (i.e. current per unit width, the 'd' in the figure)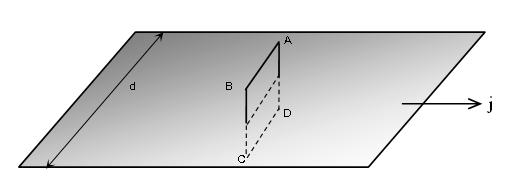
j=\sigma v
Take a rectangular loop ABCD piercing the sheet, as shown in the diagram with AB and CD being at the same distance from the plane. By symmetry, the field is going to be parallel to the sheet in the direction A→B above the sheet and in the direction C→D below it. By Ampere's law, we get
\oint_\mathrm{loop} \vec{B}\cdot \mathrm d\vec{\ell}=2B\ell = \mu_0j\ell
where AB =\ell. From here we get the magnetic field as
B = \dfrac{\mu_0j}{2}=\dfrac{\mu_0\sigma v}{2}
