3) is it B) ?
1. A wire of resistance ' R ' and length ' L ' is connected to a d.c. source of emf V through a switch ' S ' .
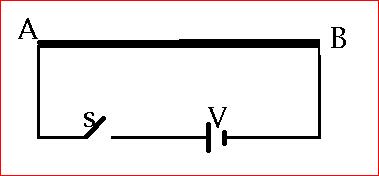
At t = 0, the switch ' S ' is closed and at the same time an external agent starts stretching the wire such that its length increases at a constant rate ' K '. Then the total heat generated in the wire due to flow of current when its length becomes ' 2L ' is :
-------------------------------------------------------------------------------------------------------------------------------------
2. An infinitely long thin metallic cylindrical shell if radius ' R ' contains positive charge of surface density ' λ ' C/m2. Then the bursting force per unit length of the shell is :
-------------------------------------------------------------------------------------------------------------------------------------
3. The separation between the plates of a parallel plate capacitor is ' d ' and its capacitance is ' C '. It is connected to a battery of emf V. Now an external agent starts pulling the plates apart till the separation between them becomes ' 2d '. If We be the work done by external agent then :
A) We > 3/4 CV2 B) We < 3/4 CV2 C) We = 3/4 CV2 D) None
-
UP 0 DOWN 0 1 11

11 Answers
Q2
2. An infinitely long thin metallic cylindrical shell if radius ' R ' contains positive charge of surface density ' λ ' C/m2. Then the bursting force per unit length of the shell is :
Per unit length ???what sense does it make
In case your question is bursting Force per unit area
then the answer must be
λ22ε0
@kreyszig
I have posted the exact question. It's in a question paper. But I don't know whether it's correct or not since I even didn't get what exactly does it mean.
@Ashish
No.
In next case, post your solution alongwith.
My reasoning was this:
Work done by external agent= -∫12Vdq
Charge flown to the battery in changing distance from d to 2d = CV-Cv/2=CV/2
Putting appropriate limits,
W=-( 1/2V[CV/2-CV])
= 1/4CV2
most probably it is having an error in printing ....
this concept is quite famous ,it is also called the electrostatic pressure

Shubodip but since the wire is being stretched, the area is supposed to decrease too right considering volume conservation?
for qstn 3....
continuing from ashish`s soln....
the initial capacitance is C and the final capacitance is C/2....
therefore,the initial energy is 1/2CV2 and the final energy is 1/2x(C/2V2)....
now by applying the work energy theorem,we get,
1/2mv2 = 1/4CV2 - We....[assuming there is a gain in kinetic enegry]
We = 1/4CV2 - 1/2mv2
so the answer shud be (d)....less than 1/4CV2....
@ashish:i think u`ve done the same thing........
for qstn 1.......
dl/dt = K
integrating,we get,
∫L2Ldl =K ∫0tdt
L = Kt
now bcoz of transverse strain the area will also decrease....[assume poission`s ratio to be 1]
so you can find the change in diameter as well....and from that initial resistance as well as the final resistance....
heat generated =Vi∫dt = Vi(L/K)....
someone pls clarify this method....
@debosmit - you cannot take out the 'i' from the integration as it is also variable.
let at any instant, L' =L(1+kt)
A' = A/(1+kt) (since vol. is constant)
R' = r. L(1+kt)A/(1+kt) = R . (1+kt)2 (r=resistivity)
heat generated = V2R' .dt
= V2 R. ∫dt(1+kt)2
= V2 kR . [1/1 - 1/2] (since kt varies from 0 →1)
= V2 2kR
sry....i did not express i as a fnctn of R....my mistake........