1)
\begin{bmatrix} 2sin\theta -1 & sin\theta & cos\theta \\ sin(\pi +\theta )& 2cos\theta -\sqrt{3} & tan\theta \\ cos(\theta -\pi )& tan(\pi -\theta ) & 0 \end{bmatrix}
The value of θ in [0,2π] such that the above matrix is skew-symmetric, is
(a) π/2 (b) π/3 (c) π/4 (d) π/6
MY DOUBT: When we evaluate elements a21, a31 and a32, won't we get that it is skew symmetric for all values of θ??
2)
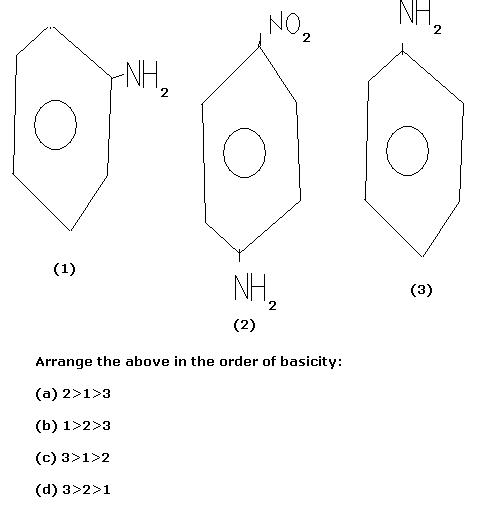
MY DOUBT: CAN ANYONE PLS EXPLAIN THE DIFFERENCE BETWEEN 1 AND 3??
1oh i am so sorry anirudh! s stupid of me! .. i shudn't have just left it like dat ....
but may be i saw u in some discussions of C++ in the forum [i may be utterly wrong.. jus' pardon me for that re] so thot u are a CS student..
anyways now thats ur dbt is over... its gr88 !!
cheers ! ~
11OH....SORRY I MISUNDERSTOOD THE DEFENITION [2]
THANX FOR CLARIFYING [4]
11As given in definition
aij=-aji for all i,j (not for i≠j alone)
so for i=j
aii=-aii(so it is zero)
Got it?
11Have mercy, sky. I'm a bio student.
How can both conditions be the same?
aij = − aji
is for i≠j. Nothing is said about the diagonal elements. Understood my doubt?
1arey! dono same hi hai !
remember wat we write in programmes of C++ ??
we go by single elements...
they have told that only..
dono ek hi baat hai....
11It's given or...so either of the conditions have to be satisfied right?
11In linear algebra, a skew-symmetric (or antisymmetric) matrix is a square matrix A whose transpose is also its negative; that is, it satisfies the equation:
AT=− A
or in component form, if A = (aij) :
aij = − aji for all i and j.
wiki defenition........ shd both conditions be satisfied?
1ani,
for skew-symm, a ij ≠a ji
but, a ij = '-' a ji
so all diagonal elements HAVE to be zero [any exception ?]
11sky, is it necessary that the diagonals elements shd be 0?
I don't think so .... cos any matrix such that aij=aji for i≠j
The diagonal elements don't matter, right?
*************edit**********
aij=-aji
12) they forgot to give NO2 or something else like CH3 etc [they only know wat !] in both 1 and 3.
so may be first one will be ortho! as NH2 is placed in such a position as if there is something.........
leave it !
11Ankit,
sin(π+θ) = -sinθ
cos(θ-π) = cos(π-θ) = -cosθ
tan(π-θ) = -tanθ
So the matrix becomes,
\begin{bmatrix} 2sin\theta -1 & sin\theta &cos\theta \\ -sin\theta & 2cos\theta -\sqrt{3} &tan\theta \\ -cos\theta & -tan\theta & 0 \end{bmatrix}
In the above matrix u can clearly see that aij=-aji for all i≠j (which is how a skew-symmetric matrix is defined)
So how does the value of θ matter???
1the ans for 1st is π/6 ... since the elements of leading dioganal is 0 at π/6
