Let S be a square of unit area. Consider any quadrilateral which has one vertex on each side of S. If a,b,c,d, denote length of sides of the quadrilateral. prove that 2≤a2+b2+c2+d2≤4. ..........[IIT 97]
Plz anyone reply how to solve it subjectively...
62The second part is easy..
the first part is also easy ;)
but just use the basic pythagoras theoryem!!
That will solve this! :O
1Take the lengths - u,1-u ; x,1-x ; y,1-y ; z,1-z ;
between 1-x and y take c
between 1-y and z take d
between 1-z and u take a
and the other b
x2 + (1-u)2=b2
(1-x)2+y2 = c2
(1-y)2+z2=d2
(1-z)2 + u2=a2
expanding and adding we get
4+2(x2 - x + y2 - y + z2 - z + u2 - u) = a2 + b2 + c2 + d2.
When x=y=z=u=0 or 1, it is max and when they are equal to .5 , it is min..
So substituting, we get the sol..
( I just can't seem to draw a proper pic in paint :()
1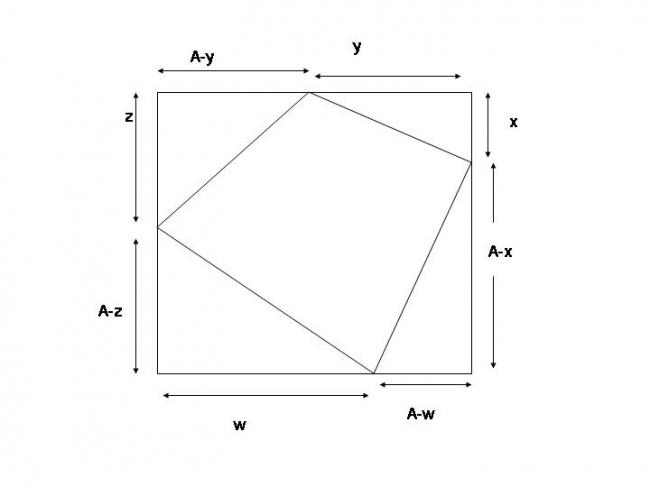
A2=1 => A=1
a2= (1-x)2 + y2 n so on..
min value of x,y,z,w .. x=y=z=w=0
so max value of a^2+b^2+c^2+d^2 = 4 .
now take a function m=x^2 +(1-x)^2
=> m' = 2x - 2(1-x) =0
=> x=1/2 is min..
so x=y=z=w=1/2 is the min value.
addind up all of them, a^2+b^2+c^2+d^2 = 4 (1/4 +1/4) =2 = min value of the expression..
hence 2≤a2+b2+c2+d2≤4.. proved :)
33Gud....
Actually objective paper solve karte karte dimag nahi chalta....
I solved it in a very shortcut method its not a method either....
thanks 4 the details...