39come on dude, do things becaus they are worth knowing. u know rolle`s therem na, i just wanted u people to know this also. its just a counterpart.
have a try.............
6 Answers
39
11If a function f(x),
(a)is continuous in the closed interval [a,b] and
(b)is differentiable in the open interval (a,b),
then there is atleast one value c in the interval (a,b) such that;
f '(c)=f(b)-f(a)/b-a
Proof:
consider the function
g(x)=f(x)-[f(b)-f(a)/b-a]x
As,f(x) is continuous in [a,b],therefore g(x) us also continuous in [a,b].
As f '(x) exists in (a,b), hence g '(x) also exists in (a,b) and
g '(x)=f '(x)-[f(b)-f(a)/b-a] .........(1)
Clearly,g '(x) satisfies all the condition of Rolle's theorem.
Thus,there is atleast one value of c of x between a and b such that g '(c)=0.
Substituting x=c in equation (1), we get,
f '(c)=f(b)-f(a)/b-a
1ohhh!!! great stuff,but as far jee is is concerned one must learn things practically(therefore visually)
Here's the graphical proof: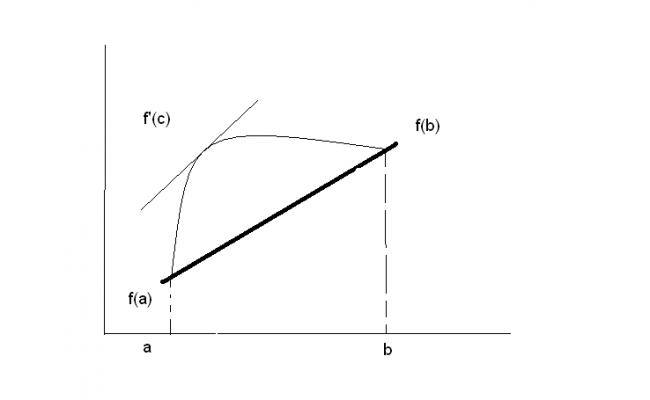
else the other proof is my using Rolle's theorem and rotating the axis
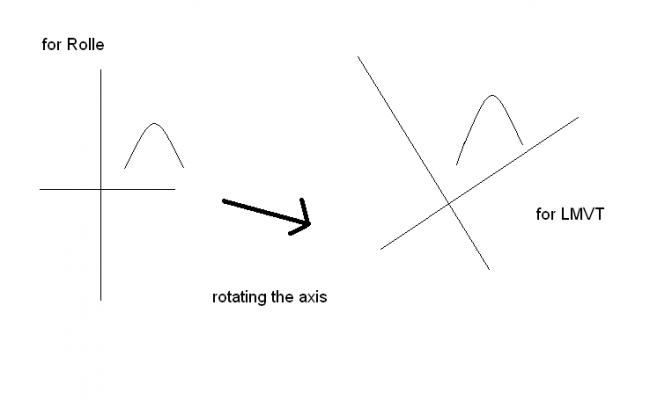
39ya i knew that there were two proofs. both rolle`s and lmvt have geometrical and normal proofs.