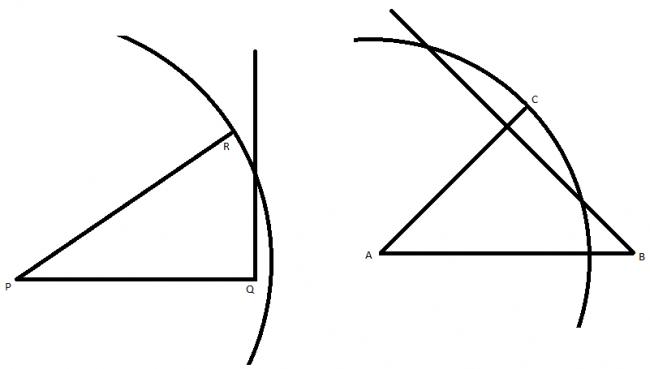36No one.....!
well that's good.....!
But there's one more criterion...
SSA
Can someone tell me that...
Is there any other congruency criteria for triangles other than
SAS
SSS
AAS
ASA
RHS
??????
-
UP 0 DOWN 0 0 8
8 Answers
36
39http://en.wikipedia.org/wiki/Congruence_%28geometry%29 says u r right
36A teacher gave me this question to solve......!!
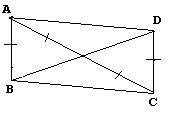
I started using the thales theorem...... by joining O with a point M on AD such that OM || AD
and thus, fooled the teacher..... he said i was correct....!!
but when i came home.... i found myself to be wrong.....!!
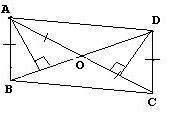
But a boy in our group did it....!!
This was how he worked that sum out....
And thus proved both the triangles to be congruent.....!!
And so i found a conclusion..... as follows......
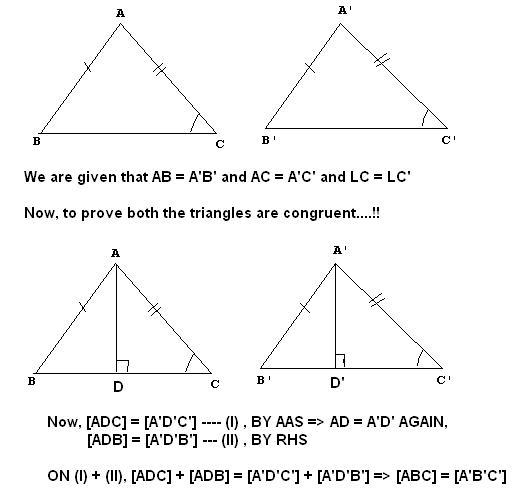
I.E., SSA IS IN A CRITERION FOR CONGRUENCY OF TRIANGLES... :)
If i m wrong... do correct me as its usual... i m always wrong
1SSA is not a criterion for any congruency
Reason : If we are given two sides of a triangle and and angle other than the vertex of the two sides than we can form two differenr triangles but in case of right angled triangle only one triangle forms and hence RHS is a congruency but not the SSA
11Hey! I'm really surprised, Practically this seems absolutely wrong. But on paper I'm unable to prove this wrong. But here's the exception- http://planetmath.org/encyclopedia/IllustrationOfWhySSAMayNotProveCongruence.html. Actually the trick in proving it is to bring the triangles together and then try to to prove congruency. That time you wont be successful.