Is it 11011 ? The number of lattice points comes out to be of the form " 4 n + 1 " .
A circle is given by the following eqn
x^2+y^2=a^2 .
Also given a is any real no.
Which of the following options may represent the total number of integral points inside the circle?
a) 11008
b) 11009
c) 11010
d) 11011
-
UP 0 DOWN 0 0 4

4 Answers
It is evident that if a lattice point lies in one quadrant of a circle centered at origin , another 3 points must lie inside it as well , which are merely its images about " X , Y " axes . Now also counting the origin as a lattice point , we can see that the no. of such points must be of the form " 4 n + 1 " .
Alternately , the number of integral points inside a circle centered at origin at having a radius " r " is given by -
N ( r ) = 1 + 4 Sigma ( i = 0 to i = ∞ ) { [ r 24 i + 1 ] - [ r 24 i + 3 ] }
where " [ ] " denotes the floor function .
Obviously , this formula easily lets us conclude that the no. of lattice points must be of the form " 4 n + 1 ".
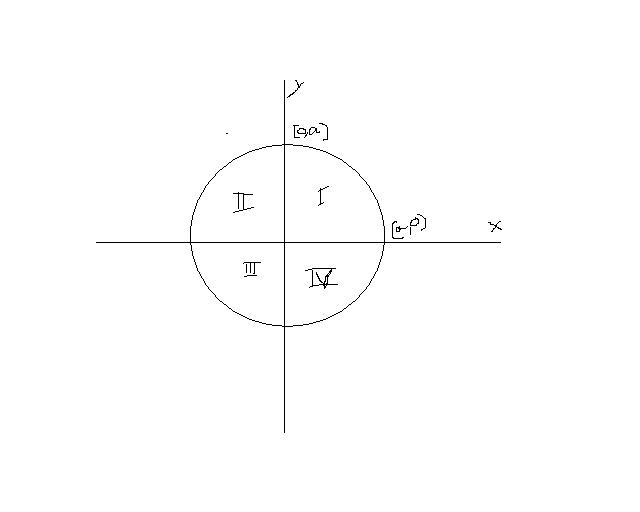
from symmetry we can see that there will be equal no. of lattice points in each of the quadrant I,II,III and IV. and centre contributes to another lattice point...
thus, the number of lattice points is of the form 4n+1, as ricky said..
here only
11009 is of the form..
so it should be the answer..