geometry lovers b555

. Triangle ABC has integer-length sides, and AC = 2007. The internal bisector of angle BAC meets BC at D. Given that AB = CD, determine AB and BC.

2. Let ABC be an acute angled triangle with AB>AC and angle BAC = 60. Denote the circumcentre O and the orthocentre by H and let OH meet AB at P and AC at Q. Prove that PO = HQ.

3. Let ABC be a triangle with AC>AB. The point X lies on the side BA extended through A, and the point Y lies on the side CA in such a way that BX = CA and CY = BA. The line XY meets the perpendicular bisector of side BC at P.
Show that angleBPC + angleBAC = 180.

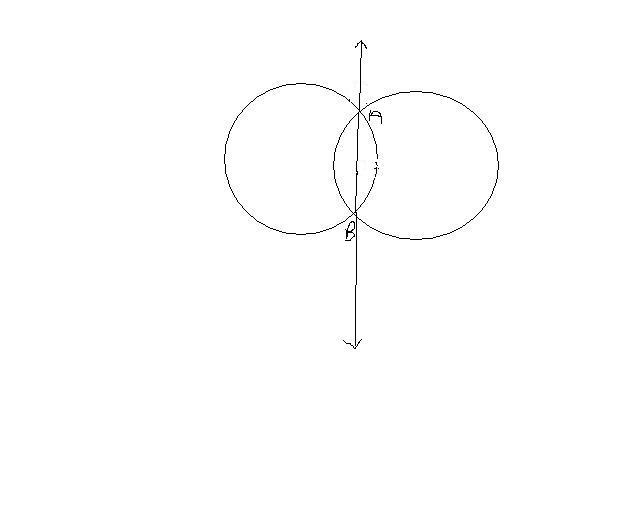
in the 1st problem, it seems to me we require that radii of the circles to be equal. Is thatt right?

as the points are moving with the same speed and return to the same point at the same time, we know they have covered the same distance in this case the circumference. so the circles have same circumference. so radius is same. so the point p as given in the question is the red point in my figure. it is half of the common chord between the 2 circles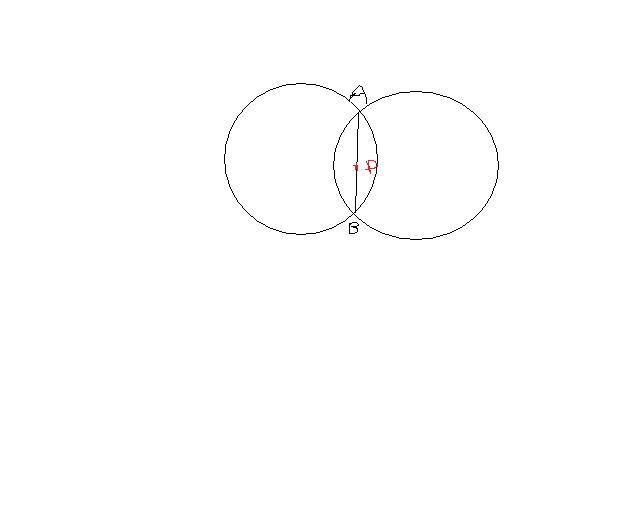
EDIt: actually it can be any point on the common chord. or the chord exted in both directions lying outside both the circles (refer to the figure below)