21y=-ln2 * ln(sinx)
only defineed for x belongin to (0,pi) ie in one full circle
11sinx>0 i.e (2n∩,2n+1∩) n is an integerbut not n∩/2
it could be written as y=loge1/2/logesinx
further
if y>0
then
sinxy=1/2
x=∩/3 , y=1
x=sin-11/4 , y=1/2
will try to draw its graph[1]
39aur bahut kuch hain yaar graph main
24I agree with mathie......[1]
1would it be useful to apply base interchange formula
& then solve?
plz say
11That is a better way da machan
11
Mani Pal Singh
·2009-03-07 23:46:50
it must be
coz there's no other way
11
Mani Pal Singh
·2009-03-08 04:47:28
mathie bata ki yeh sufficient hai
ya iss mein aur kaam karoon
39
Dr.House
·2009-03-08 04:48:15
teri marziii. anyways gud work
1
palani ...............
·2009-03-08 10:53:06
by applying base interchange formula
|y|=\log _{sin x}\frac{1}{2}
|y|=\frac{1}{log_{1/2}sinx}
let z=log_{1/2}sinx
then by plotting this graph
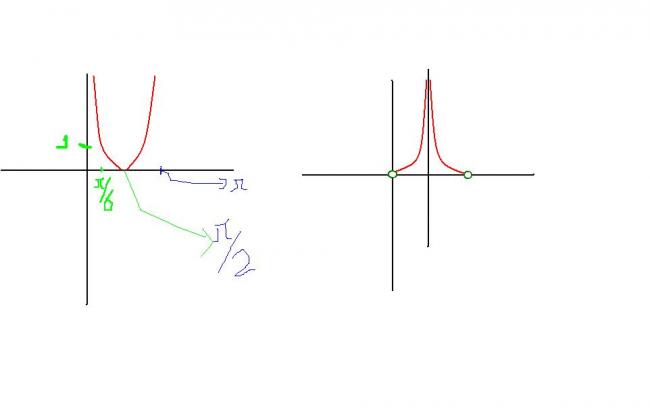
GRAPH OF Z GRAPH OF 1/Z
and inverting it is easily solvable
