my dirty graph for this question [3]
1.How do curves of following differ(if they)
a) y=log3x2 and y=2log3x
b) y=2log2x and y=x
c) y=tanx.cotx and y=1
2.Sketch the curves of following without help of calculus............
(draw the rough sketch and post it otherwise make it urself and match it with soln.after few days.)
a) y=1/(log1/2sinx)
b) logxlogyx>0
c) cosx-cosy>0
d) log|sinx|y>0
Not clicking anything
Well may be after AITS part test 2 it will click
:P
@Shailesh, no shailesh i'm a student of class 12 preparing....
That y=1/(log1/2sinx) is gr8 try it....
wait those vertical lines not in curve is of kpi/2 as sinx≠o or ±1
that logxlogyx>0 question u solved absolutily correct....
Case 1: x>1
logyx>1 so logx/logy>1 so 1<y<x will be solution.
Case 2: x<1
logyx<1 so logx/logy<1 so 0<y<x will be solution.
____________________________________________________
but graph u drew in hadbadi so only sketching is wrong for x>1
pt(1,1)is also not in graph...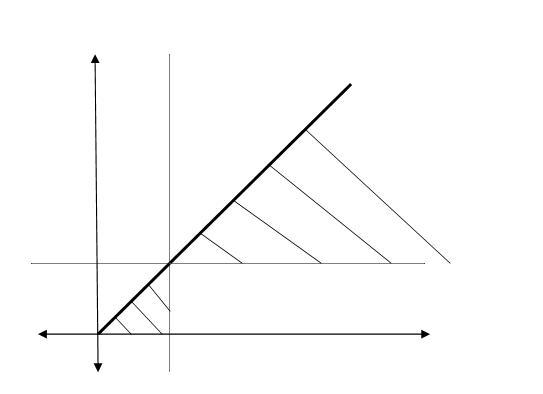
Cosx-cosy>0
u drew grayed parts as part of graph....
so (pi/2,0)is part of graph but cos(pi/2)-cos(0)<0
tills sq part that is graphs will be square it is correct but slightly displaced squares think again.
write the given inequality as products of sin terms....

in this image all white lines are not included in the graph. Also Y axis is not include. Also the gray part is only till Y=0 to Y=1
This is the solution for part d...
Abhishek tell me if it is right or wrong?
d) log|sinx|y>0
lny/ ln|sinx|
for this part, denominator is always negative. or undefined at x=2npi
so y has to be less than 1.
So the function will be like rectangles.
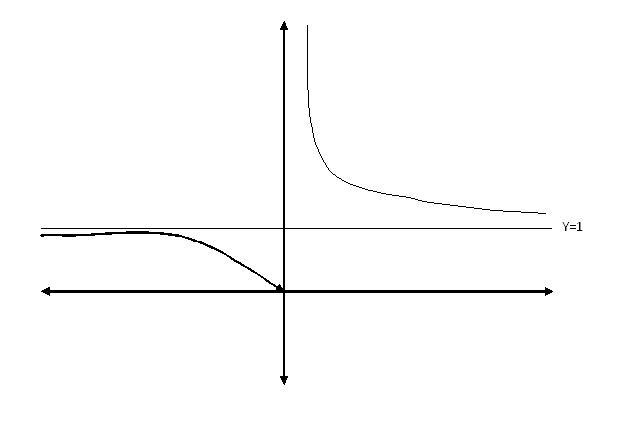
For ex curve of y=21/x
first domain of fn. is all real x except x≠0.
for x>0,
if x increase without bound 1/x decreases to 0 and 21/x decreases to 1.
for x=o+ i/x is infinitely large so 21/x → ∞
so for x>0 21/x decreases exponentially from ∞ to 1.
for x=0- 1/x is infinitely large negative. now 2-∞=0.
also for x<0, 21/x is similar top curve 1/21/x for x>0.
when x→-∞, 1/x→0- so 21/x→1-
Similar inspection for drawing curves is very useful for quick graph sketching if u practice it and get control over it.
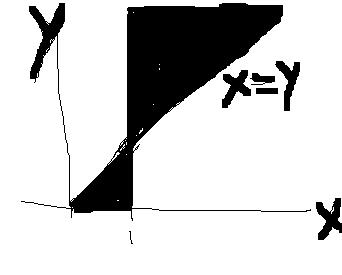
logxlogyx>0
since x and y are used in base so x,y>0
Case 1: x>1
logyx>1 so logx/logy>1 so 1<y<x will be solution.
Case 2: x<1
logyx<1 so logx/logy<1 so 0<y<x will be solution.
now back to this question. I find this one very good.. let me think and draw the graph [1]
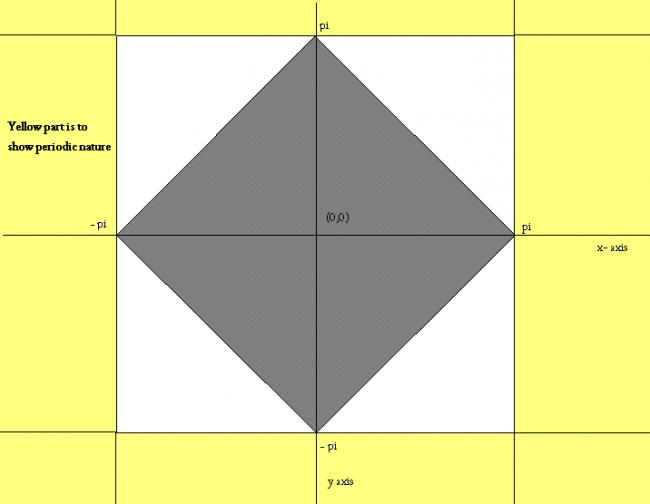
Repeat this gray area everywhere.. I think this is the graph of the functions given!
2 c) cosx-cosy>0
I think it will be lot of squares of side 2pi repeated ...
If i can draw one square from (-pi,-pi) to (pi,pi) then we can just keep repeating this square everywhere.. because it is periodic
c) y=tanx.cotx and y=1
slightly different but same difference again.. it has different domain
points n.pi/2 are not defined.
So in a, b, c the both functions have different domains.. That is the difference
b) y=2log2x and y=x
Again same difference. for -ve x it is not defined.
1 a ) 1.How do curves of following differ(if they)
a) y=log3x2 and y=2log3x
The first graph will be symmetric about x axis.. and defined for -ve x.
The 2nd graph is not symmetric and not defined for -ve x
One guess for sketching......
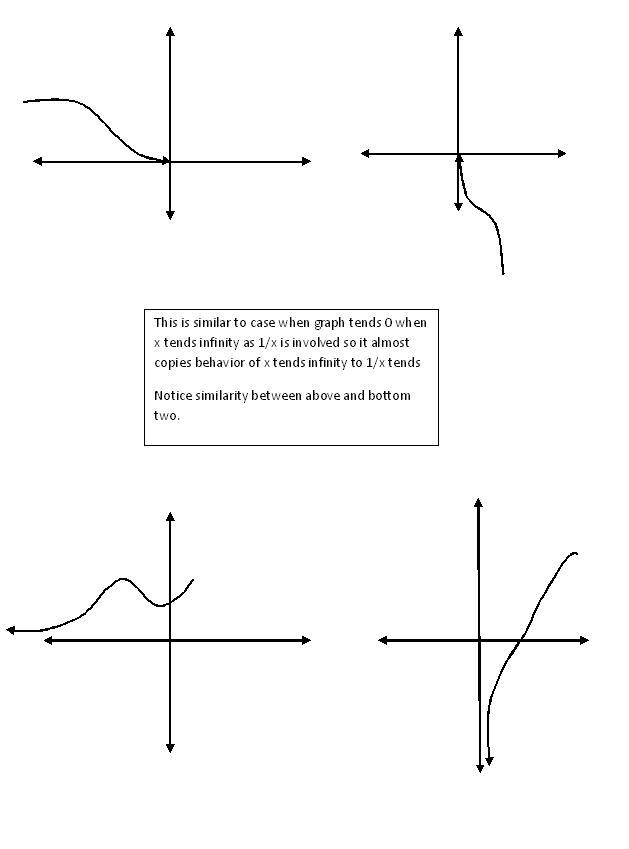
almost in every cases of basic log or exponential or similar nature curves......
these are common whenever there is 1/x type involved. Notice the point of infleections here this is also true for previous curve y=21/x for x=0-
But this is not a full proof method of finding pts of inflections but calculus may help.
This graphing technique is helpful for solving problems related to no of solns, limits and many more but not involving graph minute details.