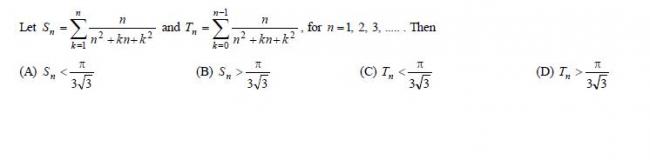iit jee concept builder

S_{n}= \frac{1}{n}\sum_{k=1}^{n}{}(\frac{1}{1+(\frac{k}{n})+(\frac{k}{n})^{2}})

T_{n}= \frac{1}{n}\sum_{k=0}^{n-1}{}(\frac{1}{1+(\frac{k}{n})+(\frac{k}{n})^{2}})

Since \frac{1}{1+x+x^{2}} is a decreasing function T_{n} is upper sum and S_{n} is lower sum. We know L(f,p_{1})\leq AREA\leq U(f,p_{2}) where p_{1}, p_{2} are any two partition on the required interval and L(f,p_{1})and U(f,p_{2}) are lower and upper sum respectively.Therefore, S_{n}\leq \int_{0}^{1}{}\frac{dx}{1+x+x^{2}}\leq T_{n}which reduces to S_{n}\leq \frac{\pi }{3\sqrt{3}}\leq T_{n}