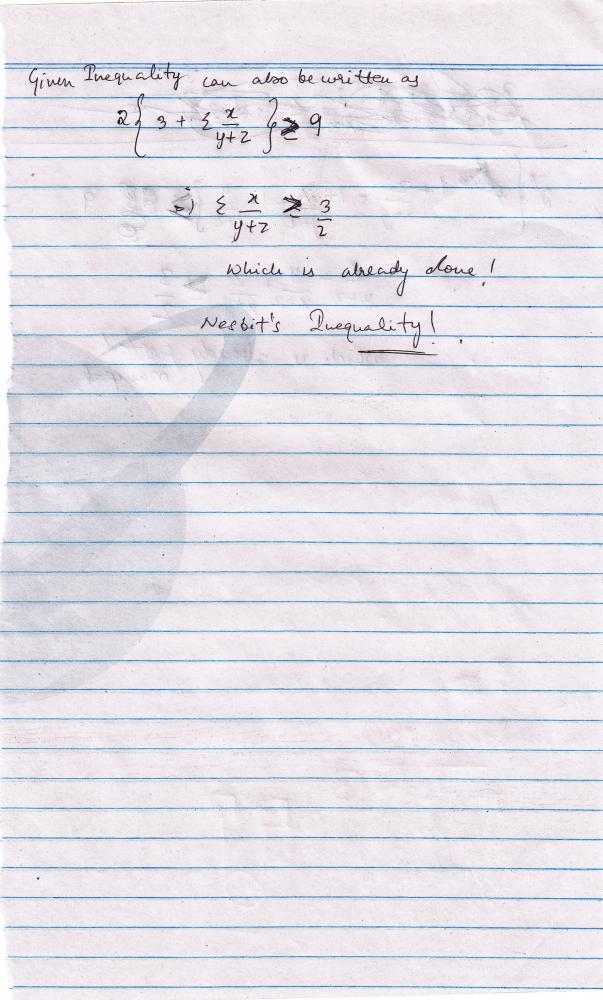39wait
Prove the following
if x,y,z>0
\frac{2}{x+y}+\frac{2}{y+z}+\frac{2}{x+z}\geq \frac{9}{x+y+z}
-
UP 0 DOWN 0 1 7
7 Answers
39http://targetiit.com/iit_jee_forum/posts/prove_it_imp_4_jee_8336.html
62anotehr proof
let (x+y)/2 = a
(x+z)/2 = b
(z+y)/2 = c
Apply AM GM inequality to a, b, c
1perhaps the same thing here :
http://www.mathlinks.ro/Forum/viewtopic.php?t=132021
______________________________________________
11sir this can also be done by CAUCHY
we can write it as
\frac{(\sqrt{2})^{2}}{x+y} + \frac{(\sqrt{2})^{2}}{y+z} +\frac{(\sqrt{2})^{2}}{x+z}\geq \frac{(3\sqrt{2})^{2}}{2(x+y+z)}
\frac{(\sqrt{2})^{2}}{x+y} + \frac{(\sqrt{2})^{2}}{y+z} +\frac{(\sqrt{2})^{2}}{x+z}\geq \frac{9}{x+y+z}
HENCE PROVED