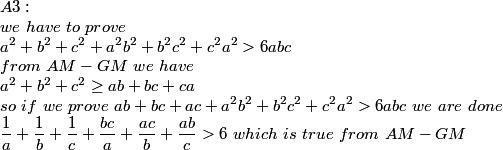1[9] i told again and again but she didnt listen .. sorry kidding [1]
I wiill put up some good questions of AM GM inequality only...
So that you all can try them.. some of themwill be very very easy.. others will be a bit more tough...
So try them all one by one..
I will try to post them in order of difficulty.
Easy one liners:
A1) \frac{a+b}{a}+\frac{b+c}{b}+\frac{c+a}{c}
A2) \frac{a-b}{a}+\frac{b-c}{b}+\frac{c-a}{c}
A3) Prove: a^2(1+b^2)+b^2(1+c^2)+c^2(1+a^2)>6abc
A4) Prove : AM HM inequality for 3 numbers a,b,c
-
UP 0 DOWN 0 1 68
68 Answers
62Tougher
C1) Minimise: f(x,y,z)=\frac{x}{y} + \sqrt{\frac{y}{z}} + \sqrt[3]{\frac{z}{x}}
C2) Prove AM GM inequality for n numbers...
C3) if a+b+c=6, Maximize: ab^{2}c^{3}
C4 (1+a1+a12)(1+a2+a22).........((1+an+an2)≥3na1a2..........an
(Eureka had given sometime back!)
C5) 2n ≥ 1 + n 2(n-1)/2 ; n is integer. Prateek gave this one sometime back)
C6) (1+a)(1+b)(1+c) = 8, prove that abc ≤ 1 (TheProphet Post 45)
App 1) Prove that the polynomial P(x) = x3-3x+2 is greater than equal to zero for x>0 (By TheProphet)
(zero means a root)
1oey!!
that i had a talk wid bhaiya ...
and i thot that we can minimise it by HM-GM or something...
but we cannot that only i told !!
[3]to all krish n philip. [3]agn [3]and again...
11bhaiya... we cannot minimise dat C3 one..
for dat we need some other condition... cos it can be as less as -∞ :P
11
A4.
a,b,c > 0
Using AM-GM for a2b , a2c , b2a , b2c , c2b , c2a
(a2b + a2c + b2a + b2c + c2b + c2a) /6 ≥ (a6b6c6)1/6
So, (a2b + a2c + b2a + b2c + c2b + c2a) - 6(abc) ≥ 0
----------------------------------------------------------------------------------------------
Now for a,b,c :-
AM=(a+b+c)/3
HM=3/(1/a + 1/b + 1/c) = 3abc/(ab+bc+ca)
AM-HM=[ (a+b+c)(ab+bc+ca) - 9(abc) ] /3(ab+bc+ca)
= [ (a2b + a2c + b2a + b2c + c2b + c2a + 3abc) - 9(abc) ] / 3(ab+bc+ca)
= [ (a2b + a2c + b2a + b2c + c2b + c2a) - 6(abc) ] / 3(ab+bc+ca)
≥ 0
Hence , AM ≥ HM for a,b,c > 0
11
C3.
a+b+c=6
a+(b/2)+(b/2)+(c/3)+(c/3)+(c/3)=6
[ (ab2c3)/(2233) ]1/6 ≤ (a+b+c)/6=1
ab2c3 ≤ 22*33 = 108
