thankx guys.
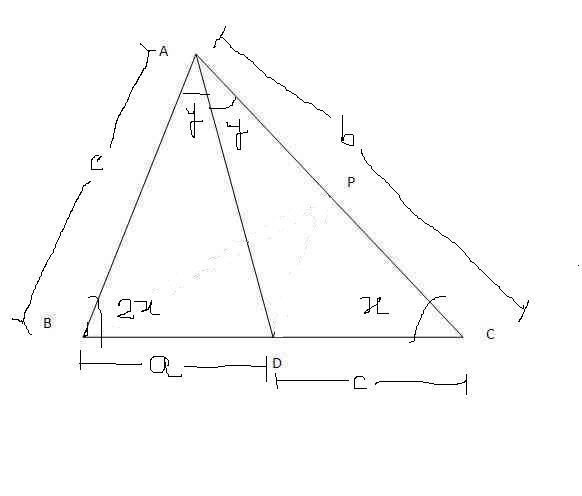
In a triangle . ABC , D is a point on BC such that AD is the internal bisector of A .If B = 2C . Prove that A=72o.
-
UP 0 DOWN 0 0 20

20 Answers
I'm not getting it , guys . help me out. couldn't go any further , problem is I'm unable to use theinfo CD=AB usefully. HOw do I proceed ,?
if U like this one U may also want to look at:
Forum » Fundamentals » AMTI october 2008
http://www.targetiit.com/iit_jee_forum/posts/amti_october_2008_207.html
Class 9 Style......
(Refer to my fig)
angle PCB= angle PBC
therefore PB=PC
then by SAS
ΔABP≡ΔDCP
angle PDC=angle A
in ΔAPD AP=PD (CPCT or whatever it is)
angle PAD=angle DAP
angle ADB=A/2+C (exterior angle = sum of int angles in tr ADC)
now angle BDC=180=ADB+ADP+PDC
(A/2+C)+(A/2)+(A)=180...............................(i)
also frm angle sum prop of ABC
A+3C=180..................................................(ii)
solve (i) and (ii) to get A=720
in tri(ABD),
c/sin(x+y) = AD/ sin2x (ang ADB= x+y by external angle theorem)
agn, in tri(ACD),
c/siny=AD/ sinx
then sin(x+y)/ sin2x = siny/ sinx
=> sinycosx + sinx+cosy / 2cosx = siny
=> sinxcosy = sinycosx
=> tanx= tany
=> x = n pi + y
but since in a triangle angles cant differ by 1 pi also,
therfeore, x= y
see fig, 5y= 180 => y= 36 => 2y= ang A = 72.
I got it in class 9 but not able now to get it....
So i searched the book and also a hint was there then after all this.....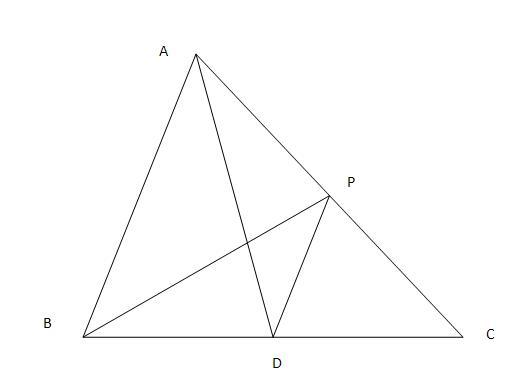
construct BP wchich bisects angle B
..........Now proceed.
Should get AP=PD in b/w.....
lol.. ye to googly hai bhai.. mere ko 5 din ho gaya ... could not get it yet :D
ABC is a triangle in which angle B=twice angle C. D is a point on BC such that AD bisects ange BAC and AB=CD, Prove that angle BAC = 720
.................................From NCERT class 9 edition 2003 pg 185 Q.20
i dun have ny idea y should it be 72????
i can (nyone can) prove dat it cant be 72 as well.....
take 90, 45, 45... and drw a internal bisector of one 45° on the opposite base...
are u missing something in this question???
is there ny other condition given.....???
do one favour,,,, write the whole question neatly once again here... plz...
I'll give my solution , please ,don't reply till then. EVERYBODY. Pleeasssseeee.
A+B+C =180
so , A+3C =180 .
by the internal bisector theorme .
AB/ BD = AC/CD
thus , b2/c = BD .
ΔADE ≡ ΔADF .
thus DE =DF
I want to prove AC =BC . is my approach right?
see I've drawn the diag and also my construction. perpendiculars to the sides AB and AC from D .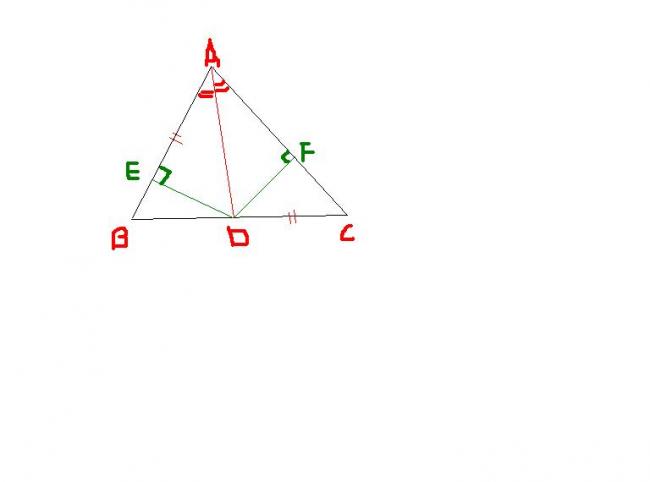
i dont understand the set up i think there is some issue with the typing !