1i m nt getting 1st ques....cn anyone plz explain.......
Q1. L1 ≡ ax+by+c and L2 ≡ lx+my+n , where a,b,c,l,m,n are real.
L1+λL2=0 represent all lines passing through intersection of L1=0 and L2=0
(True/False)?
______________________________________________________
Q2. Lim(x→0)(sin(1/x))/(sin(1/x)) = ?
______________________________________________________
Q.3 x = (2y±(2y-1-y2)1/2 )/2 is a second degree general curve here it represents ?
______________________________________________________
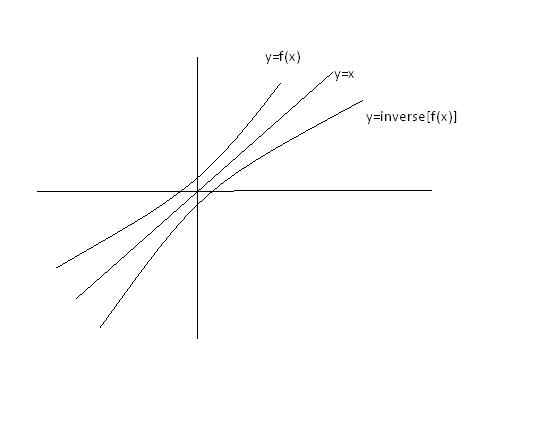
Q.4 The solution of f(x)=f-1(x) if exists lie on ?
a) y=x
b) y=-x
c) None(Specify)
______________________________________________________
-
UP 0 DOWN 0 2 89
89 Answers
13ans 2 d second q shud b 1 ...as both d num and denom behav in d same manner and will olwz giv 1.....
sum1 plz verify
21is this thread closed?
isme to hardly ek-do PINK hai......... how can it b closd?
3hey guys please help me to solve the qn4 and please explain me how the linear combination λ1L1+λ2L2=0 will represent the line passing through the pt of intersection of the two lines L1and L2. please give me a proof .
3for the second question the limit does not exist as this is approaching an indeterminate form
62Oops i messed this one again :D
lol.. damn! Deleting my posts before i make a fool of more ppl out herer :D
33What about
Lt (x2-4)/(x-2) ?
x->2
Here you can approach 2 from any path i.e. from rational or irrational or any series and you will be always in the domain of fn as only 2 is not in domain and any infinitesimal interval around 2 is in domain ...
But earlier no matter how small interval you take around 0 there are infinite points not in domain so you can't reach 0 from any path...
One example from path x=1/n*Pi . Here as n→∞ we reach 0 but these points are not in domain....
62bcos it becomes sin (infinity) i mean 1/x becomes very large..
so it starts to oscillate.. we dont know what value it will take!!
1Q1. L1 ≡ ax+by+c and L2 ≡ lx+my+n , where a,b,c,l,m,n are real.
L1+λL2=0 represent all lines passing through intersection of L1=0 and L2=0
(True/False)?
It is false because for no value of λ will we get L2=0.
We can get L1 = 0 by substituting λ=0 but not L2 which is also passing through the intersection
1Read the def of limits...
lim(x→a)f(x)=b means as value of x approaches 'a' (always keeping itself in the domain of the function) f(x) approaches a fixed value 'b'.
Oh no first Lim(x→0)(sin(1/x))/(sin(1/x)) , according 2 me limit should not exist as limit exists if the limit approach a fixed quantity no matter from which path we approach it but here we can't approach 0 with path i.e. x=1/n*Pi and a very infinetisimal interval across zero will contain numerous points not in domain. but i'm not sure......
What about
Lt (x2-4)/(x-2) ?
x->2
11ab vaale koi kaam nahi raha to iss pe comment kar lo[3]
yaar yeh to har jagah cheek cheek ke kaha ja raha hai ki 2nd ka answer 1 hai[3]
33if any one has some questions on basics (core basics) plz mention here...
First read the entire thread and comment...
33x=(2y±(-(y-1)2)/2
so y=1
then only 1 point naa (1,1)
Most of the work u did but jaldi me tune gadbad kar diya...
thoda calm raho
33Don't U think the expression under bracket is
(-(y-1)2)1/2
so ..............
33Now 3 questions have lead 2 good conclusions now last question of the topic is left but an easy one...
1ans 4 is c......y=x
solution of f(x) and its inverse if present lie on line y=x......thus solving f(x)=its inverse is the same as solving f(x)=x provided function is not piecewise defined
but if no solutions exist then f(x ) and its inverse will not intersect at y=x
106@Aditya : please see the wonderful discussion in the previous page regarding the last question
262in the last question, all the functions which are symmetric about the line y=x will satisfy the given condition always for eg. xy=1
this is because graph of f-1 (x) is the reflection of y= f(x).
hence if f(x) is symmetric about y=x, f-1(x) will always be the same as f(x) .
hence this is just a case of exception , otherwise the soln. always lies on y=x
33The solution of f(x)=f-1(x) if exists lie on ?
the question specified "if exists"
1The last one was a googly, if there are no solutions it will not lie on y=x.
Consider the example below.
Answer: None
