1
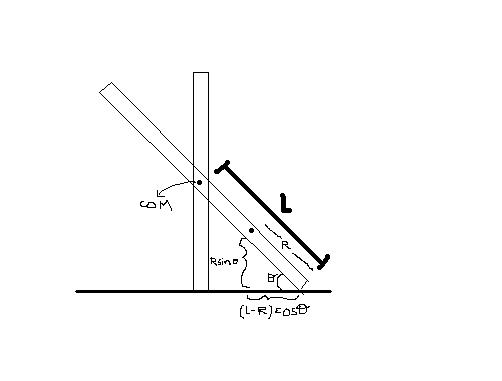
since the surface is frictionless the COM always moves along the line x=0.
if the coordinates of the point R be (x,y) then
(L-R)cosθ = x and Rsinθ = y
eliminating θ, we get locus of the point as
x2 / (L-R)2 + y2 / R2 = 1 which is an ellipse
a uniform rod of length 2L and mass M is kept vertically (along the Y axis) on a frictionless surface. its end point is at origin.. suddenly its end point starts sliding on the plane along the positive X axis..find the locus of the point which is at a distance R from the end point..
-
UP 0 DOWN 0 0 7
7 Answers
1
21alternative: (l/a) =(r-l)/x
(x+ a )^2 + y^2 = R^2
eliminating a,we get the equation///
1@euclid : hey there is a mistake in the fig.... the length which u 've marked as (L-R)cosθ is wrong... it will be the length measured from the origin.. nd nt from the base of the rod....
11maine isko IOR se kiya hai.
(waise jor jar kar bath waisi hi hai.)