so if
one particle has y=asin(wt +θ)
then other has y1=asin(wt+θ+Π/3)
thus max is y1+y
and min is y1-y
right?
plzzz help me out with the basics of SHM & WAVES....
I am stilll very weak in this topic of physics...
help me out with the basics of the topic...
for the phase difference wala sum...
as u asked..
the maximum distance is given by:
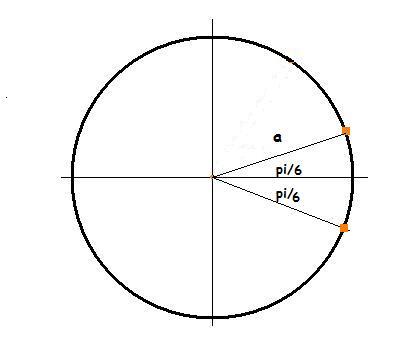
So this case, as we discussed gives maximum distance..
and maximum distance, thus will be = 2.a.sin(Ï€/6) = a.
anyway another sum:
Q: 2 particles are performing SHM on same track side by side. Phase difference between them is π3 and their amplitude is a. Then find the minimum and maimum distance between the two particles.
Given: They have same ω.
so if
one particle has y=asin(wt +θ)
then other has y1=asin(wt+θ+Π/3)
thus max is y1+y
and min is y1-y
right?
yeah.. but geometrically, i.e. using reference circle your life will become lot easier..! :P
okay... (firse draw karna padhega!!! :O :'( )
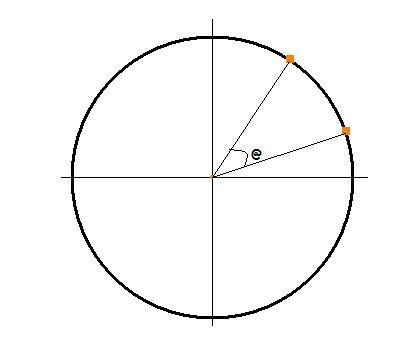
So this is the condition .. here @=phase difference...
The shadow on y axis will have maximum distance when the two particles are present symmetrically on either side of the x-axis and will have minimum distance when they will be place symmetrically on the either side of y-axis..
Try to visualize the two situations then things will become clear! :)
cheers!
Anyway do the other some yet lurking here untouched!
to that qestion where t=5sec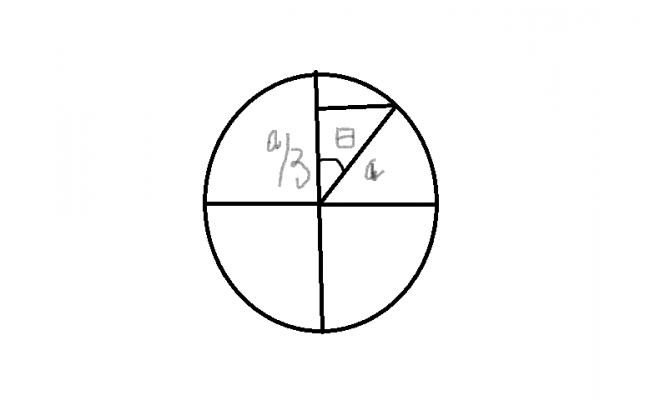
now
y=Asin(5w + cos inverse 1/3
is this the answer??
Anyway I continue:
this time I am starting "babes" :P (I mean waves)

In the figure shown, the mass is in equilibrium ant the rod (through the spring) makes the constraint that particle won't move along horizontal direction. It means the net force on the mass along horizontal direction will always be 0 i.e. the force exerted by the string on the mass towards right is equal to the force applied on the block by rod towards left.
Now if we apply a sharp impulse on the mass then the particle will perform SHM. Now, the first point of the string (which is common to both the string as well as the object) will also perform SHM. The next adjacent particle on the string will also perform SHM.
For the motion of the second particle on the string (referred to in the last senlence of the last paragraph) only the string is responsible.
Hence, we can say that a special kind of force has been generated in the string such that particles of the string perform SHM.
Since, this force is acting on all the particles of the string, hence, all particles of string will perform SHM and a kind of disturbance (wave) is produced in the string which is called HARMONIC WAVE or SIMPLE HARMONIC WAVE. (i.e. my BABE :P)
The snapshot of the string at various times given wave is started at t=0.
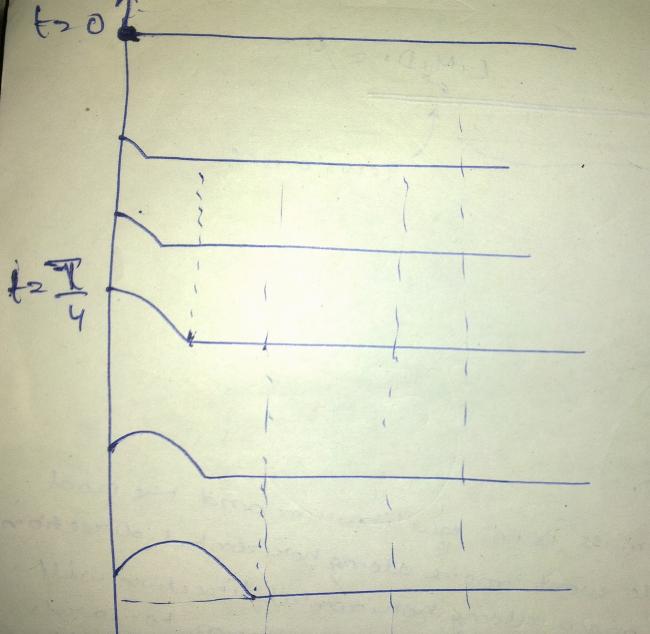
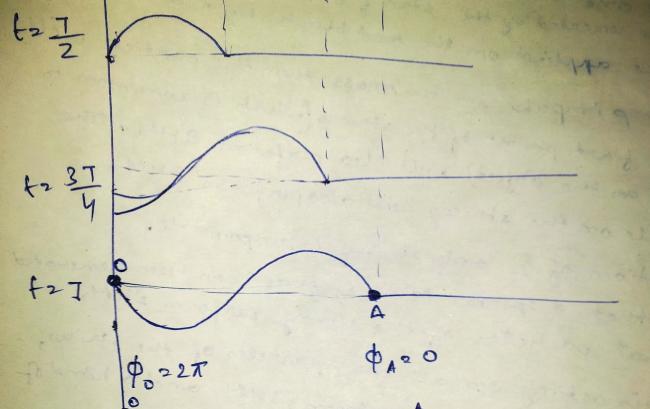
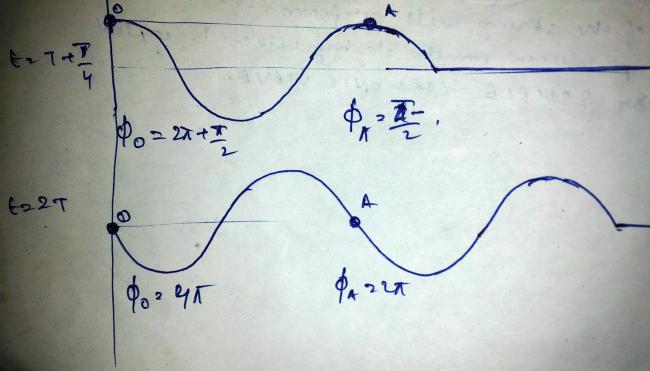
Once the wave reaches a particular point , then onwards the phase difference for this particle and any previous particle from where wave is coming will always remain constant (time independent).
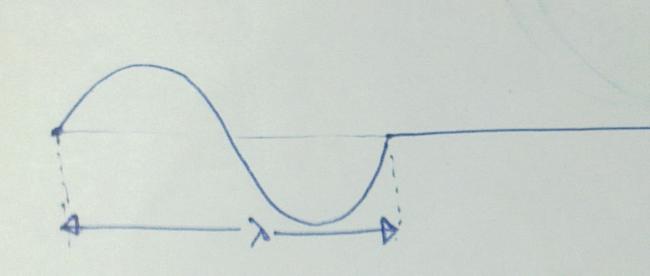
Distance travelled by wave in one time period is called wavelength.
In T seconds wave travels λ units distance.
So, in 1 second, it travels λT units of distance = ν.λ [since 1T = ν (frequency)]
thus, velocity of wave (u) = ν.λ
thus
u=νλ
Again..from previous post, let us compare path difference and path differences...
Path Difference Phase Difference
λ 2π
1 2πλ
x 2πλ.x
aacha.. in case of waves will it continue to be in ... a circular motion along a fixed point..???
what is the work of the spring in this case..???
what do u mean by phase difference...???
i mean..... does the change in path difference change the phase difference........??
aachha in the case of the string why will it undergo such.... type of distortion.....
i mean partly its straight..... and after that it bends.....
why not lyk this pic???
now
displacement is negative but vel positive i.e.4th quad.
θ=Π/3
therefore phase = 3Î /2 + Î /3
i.e. 11Î /3
therefore equation is
y=Asin(wt+11Î /3)
is tat correct?
For SHM first of all we will have to consider a reference circle... (to make our lives easy obviously)
Consider the following particle start its circular motion in a circular groove with radius A when it is at an angle θ from the x-axis (anticlockwise direction).
Suppose it is moving in an anticlockwise sense with an angular velocity of ω.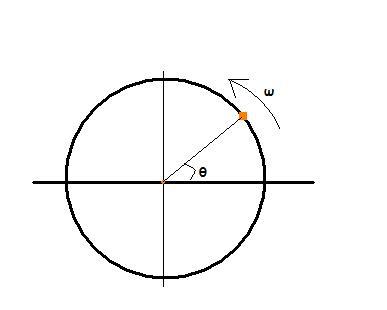
Now after time t, the particle makes a polar angle of θ+ωt with the x-axis..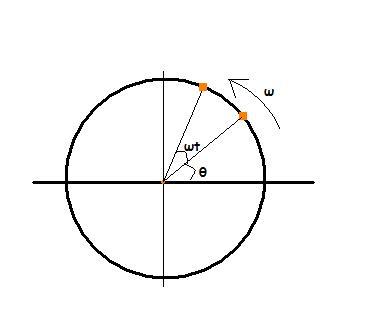
Now we will consider the projection of the particle on the y-axis.
And find the equation of the position of the shadow with respect to time.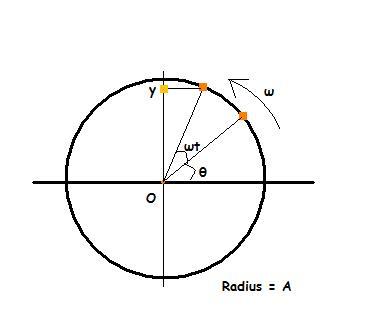
by basic sense of geometry, we can see the triangle formed by origin, the particle and it's projection is a right angled triangle.
and by basic trigonometry we know that:
y=Asin(ωt+θ) ------(i)
differentiating both sides w.r.t. time..
v = Aωcos(ωt+θ) -------(ii)
Differentiating again...
a = - Aω2sin(ωt+θ) -------(iii)
From (iii),
a=-ω2y
(that is satisfying condition of S.H.M..thus the projection is undergoing S.H.M.)
Thus, we can consider equation (i) as general equation for S.H.M
also, from (ii),
v=Aωcos(ωt+θ) = ω.√A2cos2(ωt+θ) = ω√A2-y2
Thus, the general formulae of S.H.M. have been derived. Now it's time for some concepts..! :D
plz help me out........... how... the velocity of a wave depends upon a string...??
is it due to elasticity & inertia.?? if so then ,,, how???
A particle's position is given below at time t=0.
It is undergoing S.H.M with amplitude A.
Write down it's equation...
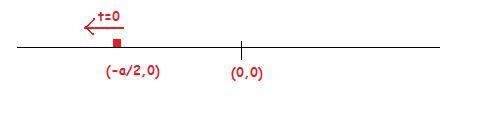
(Arindam...A sum for you..)
Okay... if that is what you want...
Let us derive it..:

Suppose I asked my sister to pull the above string with a force Fx as shown in the figure..
So the tension generated in the string T=Fx.
Let the linear mass density be μ.
Now, suppose I started pulling the string in the upward direction, as shown...
the string will undergo the following deformation (i.e. a pulse will be generated).
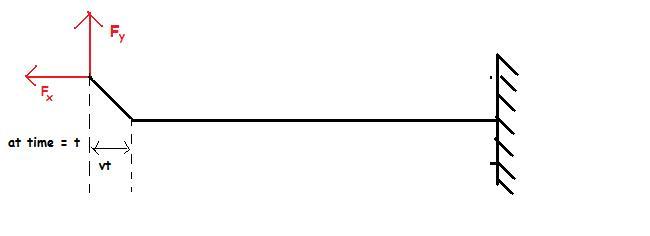
Fy.t = m.vy
mass of string having velocity in y direction after t time is μvt (from figure)
so, Fyt= μvt.vy
or, Fy = μ.v.vy
since every other term in the above equality is constant,
vy= constant.
(this can also validated by newton's second law.)
F=dpdt = mdvdt + vdmdt
dvdt = 0
so, Fy = μ.v.vy
now, the resultant of Fx and Fy must be along the deformed length of the string (why?)
thus, FyFx = vytvt = vyv
or, μ.v.vyT = vyv
or, v2 = Tμ
or, v = \sqrt{\frac{T}{\mu }}
T is the elastic factor of the string...
while μ gives the inertia factor of the string...
So, I hope your question is here answered!! :)
@subhomoy: please continue ur explanation.i need it badly.
thank u.
oh u were going great.
Okay, so I will continue from my last question post...
The particle has negative displacement and moves towards negative direction....
thus in our reference circle the particle must lie in the third quadrant...
( negative displacement means located below the origin and negative velocity means moving downwards...)
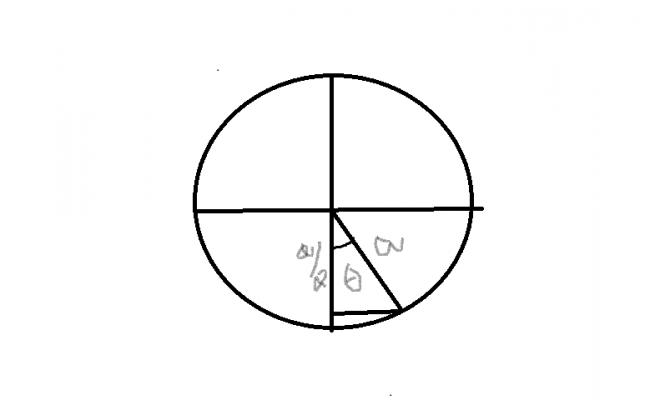
Thus, the particle resides in the third quadrant with it's shadow on y axis at a/2 distace from the origin...
Lets see the reference circle..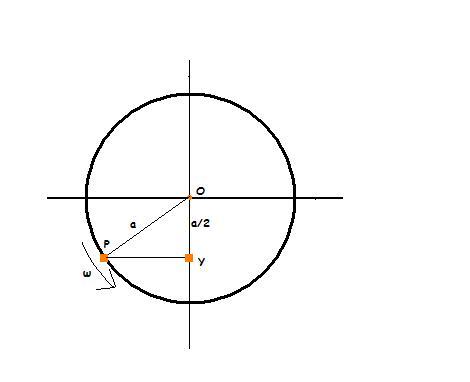
angle POY = cos-1a/2a = cos-112 = π6
So, phase angle (θ) = 3π2 - π6 = 4π3
So, the equation is: y = Asin(ωt+4π3)
Hope that clears many thing..! :D
Next question:
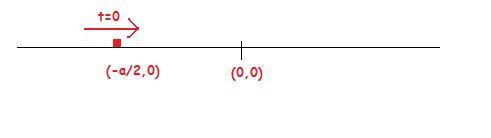
Write down the equation of the particle undergoing SHM.
yaar mera bhi ek mistake the cos-112 = π3 not π6 :P
anyways.. disregard...
I ll continue! :)