1)
------------------------------------------------------------------------------------------
2)just a doubt....
my doubt is shud'nt it be 4 common tangents
???
39Arey mere pyaare munna pyaare mohan anand...ek circle ki tangent condition mein do tangents possible hain because of two values of m....do you know that we are discussing common tangents beta?
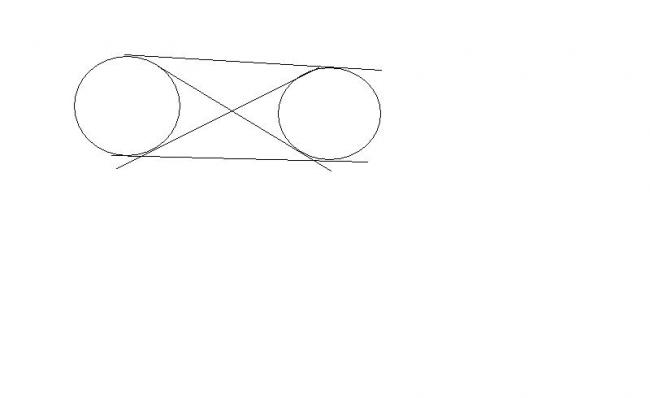
When you see that two tangents are possible for BOTH circles, you will see that in overall 4 tangents are possible for the circles as a pair.
Betaaa...mann mein laddu phoota? Cadbury dairy milk shots...ek packet mein do goli :P
1@karan and joydoot
i already told that see post no. 5 of same thread[3]
11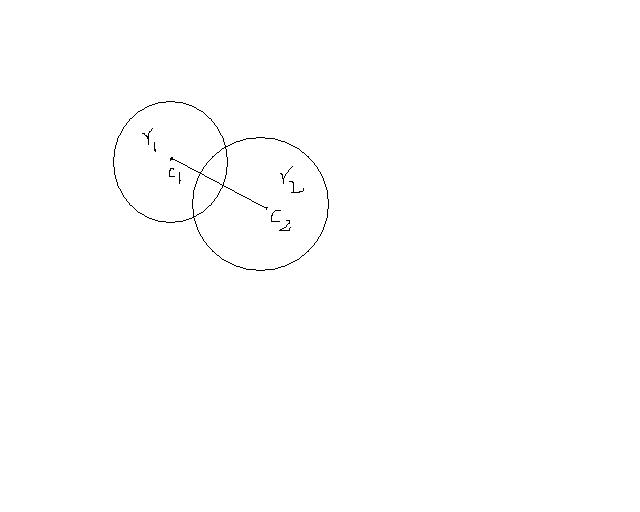
cleary , C1C2< r1 + r2.
thus, there should be two common tangents...
yup karan, u r right..
1unless i miss out on something largely, this shud be 2 only.
look c1c2 < r1 + r2
sure , the circles do not touch but THEY INTERSECT at 2 distict points.
so 2 CT.
1i think it is 100%
mv12/2=K1
mv22/2=K2
K1
K2=3K1 + K1=4K1
v2=2v1
p2 = 2p1
p2= p1+p1
hence 100%
23http://www.targetiit.com/iit-jee-forum/posts/all-time-doubt-service-15095.html
1ha ha pritish gud one
YES definitely 4 tangents wuld be there i thnk answer in arihant is wrongly printed
I'm sure tangents number that can be drawn with the derived condition as per books solution is 4
11.D
2.common sense LOL![btw i din solve it[3][3]....but u just need to do use some equations n expressions property[1]]
11oh....ya..i got my mistake...so... bhaiya can you post the method please......for the 1st one...plz..plz...
23@ sandipan , KE of a particle depends on its mass also, so if KE has changed, u cant rule out the possibility that mass has also changed
11bhaiya plz point out my mistake.....plz plz bhaiya......[2][2][2][2][2]
1lagta hai ki u need to study DHYAN se differential calculus again[3][3][3]
11for 1 plz plz plz plz....kindly post the sol'n...this is how i proceeded..where's my flaw???
P=√2mK
dP = √2m dK2√K
dPP = 12 dKK
(dPP x 100) = 12 (dKK x 100)
% change in momentum = 0.5 x 300%
= 150%
plz point out where i am wrong....[17]
1baccha log 4 tangent ka to sawal hi nahin uthta [3].....
sirf first circle ki tangent ki condition dekh lo :::
(y+4)2+m2(x+1)2-2m(y+4)(x+2)=42(1+m2)
ab at the most to ONLY TWO POSSIBLE VALUES OF m are there from FUNDAMENTAL THEOREM OF ALGEBRA[3][3][3][3].......
39Yeah.. shouldn't there be two direct and two transverse common tangents? The direct ones are parallel(visualise) to each other and the transverse ones cut each other at a point.