106mathie which graph.. (1) or (2)? (2) im perfectly sure.... 1 hr baitha ha us par sirf d2y/sx2 nikaalne mein...
21 Answers
106
21thnx asis!!!! got ur pt.
write man! hadnrt read post 10 earlier jus saw ur graf!!!
write write !!! only int, int satusfy!!!
106bhaiyya thats what i have written in post #10.... isnt that correct?
3Nishant sir...
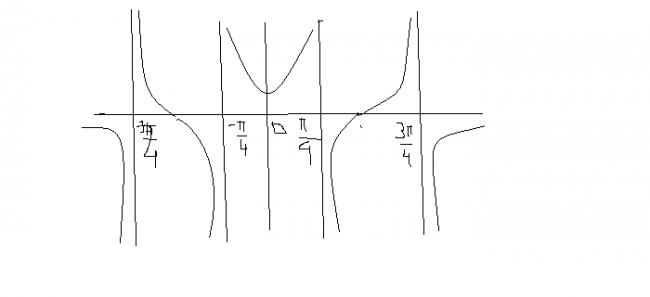
is graph 1 as drawn here correct ???
I feel, the only solution is (x,0), where x is any integer....
62bhargav.. i think you have slighty gone wrong!
at x=0 cosx/cos2x=1!!
as x-> pi/4 LH Limit
cosx-> 1/√2
while cos 2x- > 0+
so the limit will tend to + infinity!
106mathie put x=Ï€ in the graph equation.
u get y=-1/1 which is definitely below... not above...
392nd one, wat i am getting is that ∩ will bne exactly above and concave upwards and those half lines at extremes should be mirror images{i mean downwards in lower half}
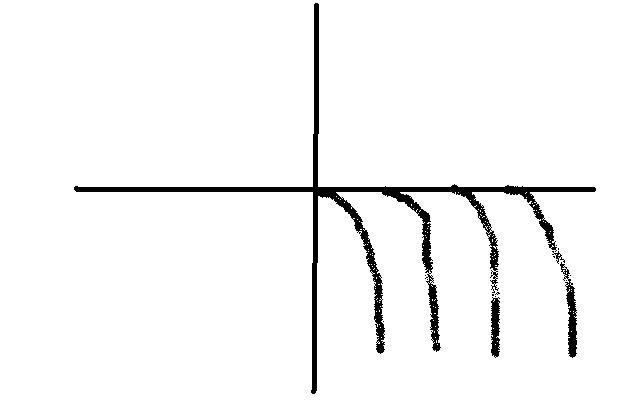
21for 0<x<1 same as kal ka graf!! xy = x+ y;
the function is periodic with integers......
39asish are u sure with the graph? check once, kahiin kuch upar niche toh nahiin ho gaya.
106graph 1.
{x}{y} = {x}+{y}
==> {y} = {x}/({x} -1)
Now, {x}-1 is always negative as {x}<1
So, {y} ≤ 0 {y}=0 when {x} =0
But{y} is always ≥0
Combining these two,
we get {y}=0 and {x}=0
i.e. the graph is only all integer points...
106maine bahut kuch likhaa tha par accidentally cancel press kar diya... :(
im not going to rite much now again.
just graph is symmetrical abt y-axis.
dy/dx=sinx(1+2cos2x)/cos22x... depends upon sinx.
d2y/dx2 is very complex.. i cant write...
at x=2nÎ , y=1
at x=(2n+1)Î /2, y=0
at x=(2n+1)Î , y=-1
discontinuity at cos2x=1/2
if cos2x = 1/2- then y=-∞
if cos2x = 1/2+ then y=∞
bada khatarnaak graph hai
by periodicity rest of graph is decided.
21no sir da graf is 4 first part, u askd naa how wud it luk!!!
2nd part graf is cont decreasing!!!!!!!!!!
21part 2...
let cosx = u;
y = u/(2u^2-1)
so discont at u^2 = 1/2;
range of u [-1,1];
112)
we have to remember the graph is not valid for x=nÎ /2 + 2nÎ
at x=0 y=1
at x=Î /2 y=0
