11For The graph between (0,1) There will be no graph 0/x =0
For (1,2)
[x] = 1 which is a constant
let u = {x}
y = 1/u
yu = 1
This the graph of the rectangular hyperbola with lowest value 1
For (2,3)
y = 2/u
yu =2
it is also a hyperbola with lowest value = 2
For (-1,0)
y = -1/u
yu = -1
it is also a hyperbola with highest value = -1
For (-2,-1)
y = -1/u
yu = -2
it is also a hyperbola with highest value = -2
For (-3,-2)
y = -1/u
yu = -3
it is also a hyperbola with highest value = -3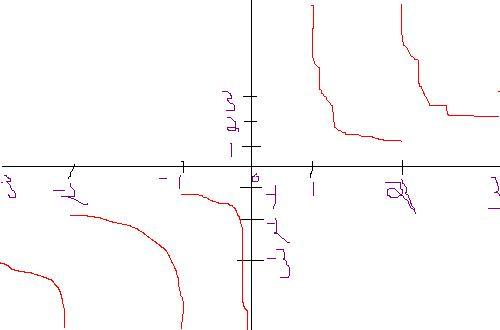
11is my graph rite sir
The hyperbola in the solution mean a part of it
11na ji na
study the definition of {x} again and den try the question!
1rite side is right ..left mein gadbad hai :)
take
-1.2
so [x]=-2 ....n {x}=.8............
n so on
24looks like everyone forgot abt this one.....
just completing it...
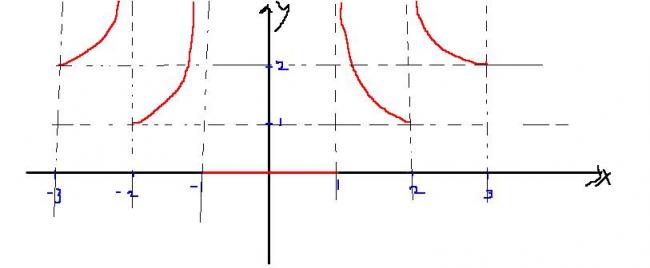
the red lines indicate graph..the black ones are just grids
62no eureka..
you have done a fantastic job.. but you seem to have missed something on the left side..
what is it?
62Virang;s graph was very good.. he just overlooked a small thing as pointed out by mrunal..
24yeah it will be in 3rd quad and not in 2nd..but nay other mistake ?
1eureka,den make corrections and post d graph again