Daily Graph 20-07-09

@asish [y]=sin²x shud exist fr x=0,∩/2,∩only as sin²x mst be an integer only .so sum editing reqd

As there have been no changes to the question, assuming that it is correct,

In the interval (0,∩), the graph comes out to be

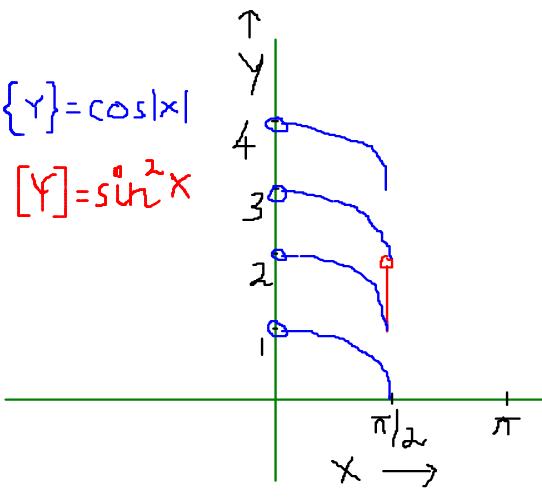
In (0,∩) sin²x is integral only at x=∩/2=1 =>y= [1,2)

In (0,∩), cos|x| is a positive fraction only for x E (0,∩/2]

Between y=[0,1) the graph is the same as y=cosx

in [1,2) the graph is as y=1+cosx

for the interval, [2,3) the graph assumes y=2+cosx

and so on, using {y}=y-[y]

These two curves only intersect at one point, (∩/2,1)

So the answer is, (∩/2,1)

[339]