11ACCHA JI .............
REPLACE x BY y
WE GET x4-y4+xy=0
adding both we get xy=0
but i am only getting i point x=0 and y=0 (by putting )
11CONTINUING THE ABOVE POST
We observe here that
\frac{\partial y}{\partial x}=\frac{4x^{3}-y}{x+4y^{3}}
The original equation is
(y^{2}-x^{2})(y^{2}+x^{2})+xy=0
we get (0,0)
and we observe here that we cannot get x=y
I AM NOT GETTING NY SOLUTION BEYOND THAT
IF THE POSSIBILITIES EXISTS
PLEASE TELL
62(y/x)4-1+y/x3=0
limit x-> infinity (keeping y/x constant) we get
(y/x)4-1=0
so y/x = ±1
so there will be two asymptodes at infinity which will have slop +1 and -1
Now can you try guys?
21apart frm the Asymptotes that u found wat else can V find Sir?
We get local Max/Min/Pt. Inflextn at all points satisfyin y=4x3
11@ NISHANT SIR
Sir ab to kripa karke isko bata do
Bechara latka pada hai[3]
66As x and y both appear with 4th power, the graph is going to be symmetric w.r.t. the x and y axes both and hence about the origin. So if we could draw the graph in 1st quadrant, we can simply mirror that on the y and x axes to obtain the required graph. As already pointed out in #7, the asymptotes are y=±x. Further, one can see from the same post that
(y/x)4=1-(y/x3) < (y/x)4
Hence, the curve approaches the asymptote from below in the first quadrant.
Again setting x=y, we obtain x2=0. So the curve meets the the line y=x only at the origin.
The first derivative
y^\prime = \dfrac{4x^3-y}{4y^3+x}
vanishes only when y = 4 x3. But setting y = 4x3 in the original equation gives
44 x12+3x4=0
the only solution of which is x=0. However, at x = 0, the derivative turns out to be indeterminate.
On the other hand, if we transform to polar coordinates by setting x=r\cos\theta and y=r\sin\theta
it is easy to show that the polar equation turns out to be
r^2=\dfrac{1}{2}\tan2\theta
from where it is easily seen that at \theta =0, r=0 so that curve takes off the origin horizontally.
In fact from the polar equation, we see that as \theta increases from 0 to \pi/4, r increases from 0 to ∞.
From the polar form, it is also obvious that as θ increases so does r. Hence the curve is strictly increasing in the first quadrant. Taking into account that r varies as square root of θ, we get the required graph, ultimately as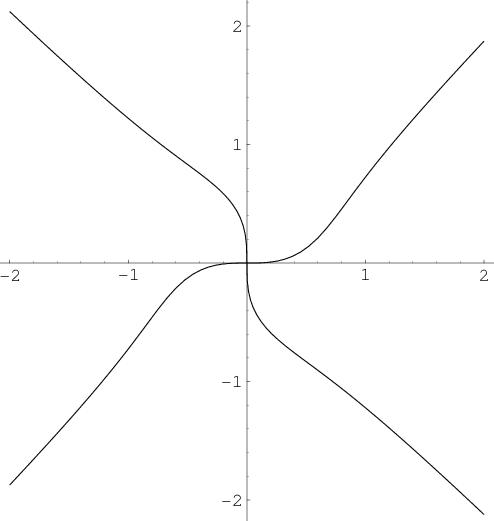
11Sir do we have to use polar form in such cases?
Wat Nishant sir meant in #7 and #9 den?
