find the range of 'b' for which the equation,
(x+3)^{2}=5-\left|x+b \right|
has 2 real solutions.
11Suppose |x+b|>0
dydx = 2x+6, hence the line y+x=5-b is a tangent to the curve at x=-72, thus min b=74.....
While if |x+b|<0, then slope of line becomes 1, meaning dydx=1 at x=-52, thus b=-94
Thus ans should be (74,∞) U (-94, ∞)
Pls correct me if wrong.
1soumik, if ur answer is (-∞,-9/4) U (7/4,∞), then plz recheck,
becoz, 9, that is in ur range of 'b' has no real solutions for the equation.
any more takers?
62soumik, for these questions, graphs come in very handy... try using graphs :)
1yeah soumik, as a matter of support to what sir has said, this has been posted under the 'graph' section. so a graphical approach always is much much easier than solving it without one :)
1plz recheck asish, for b=8, we do have solutions, {-3,-4} both greater than -8.
106
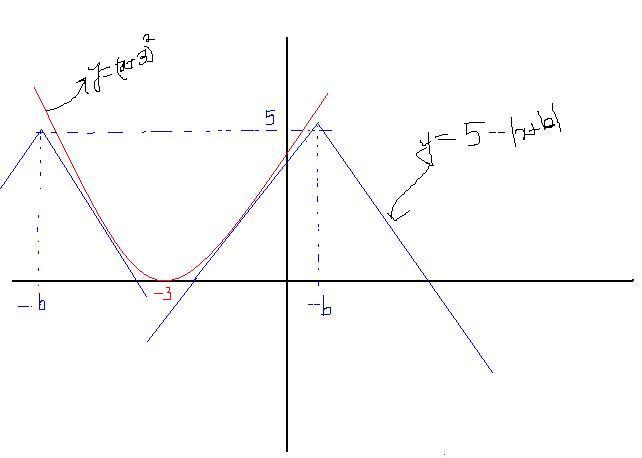
So there will be two solutions if b will lie between the two points shown on the graph.
Now the y-coordinate of the point (-b) is 5. let the two abcissae be x1 and x2
Let y=(x+3)2
dy/dx = 2(x+3) = 1 when x=-5/2
dy/dx = -1 when x=-7/2
So the tangent points are (-5/2, 1/4) and (-7/2,1/4)
So, lx2-(-7/2)l = l5-1/4l and lx1-(-5/2)l = l5-1/4l
So, x2 = -7/2-19/4 = -33/4 and x1 = -5/2+19/4 = 9/4
So, -b = (-33/4,9/4)
So, b = (-9/4,33/4)
1i was getting (-9/4,33/4). donno whether there is a silly mistake or what. (on our part) :)