106nice work subho...
but can you try to give a quantitative description (although it is not necessary for JEE aspirants in any way)
Here's a doubt from my XI days that hadnt been solved till recently possibly bcz i hadnt given much though abt it.
THe question is as follows
Q. Consider a smooth rod revolving about one of its ends on a horizontal frictionless table with a constant angular velocity ω. A smooth bead is inserted in the rod and the rod starts revolving. As expected, the bead shoots out of the rod with considerable speed.
The questions are:
(1) even though there is no force in the radial direction, (rod and bead are smooth) yet the bead has a non-zero radial acceleration. explain
(2) quantitatively give an expression of the bead's radial acceleration and radial velocity in terms of ω, r and ro (at r=ro, v=0)
Give the differential equation instead.
-
UP 0 DOWN 0 1 10
10 Answers
49actually no!
i can try to explain this like :
The rod is accelerating(i.e. chaging its velocity's direction!)
and the bead, by virtue of its Inertia tries to remain it its original position...
so there is faces a normal force from the rod it is the only force possible due to absence of friction...
but see now...
when the force is applied in the next instant the rod has moved by some angle and as a result, there is a component along the radial direction which can now explain for the non-zero radial velocity! :D:D
(Don't kill me for this! :P Please! :D)
10649quantitative as in?
matlab involving equations?
well have to work on it a bit b4 posting that!
will try to do that at the earliest! :)
1
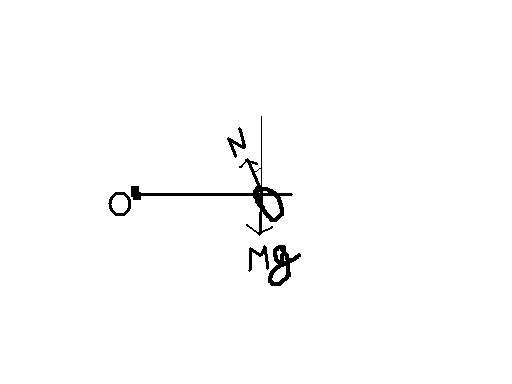
considering bead has some mass...so its orientation will not be " straight" when rod is rotating......i.e when the rod is rotating is will be slightly titted ...... , so cos component of normal would balance its weight....thus having a sin component for providing radial acceleration....
i.e
N cos (theta) = mg
N sin(theta) = m w2r
1
image on the right confirms that when rod is rotating bead's orientation will not be straight......
49@bornidentity: if that had been the case, would nt the bead prefer remaining static instead of sliding?
as of me, in the above solution i find it hard to imagine a flat (or straight) wire with no friction providing an oblique reaction force (and even if it is possible it is in no way a NORMAL reaction!)! :( to me that seems so unlikely! :(
tell me if i am wrong!
1
see the image of the "merry-go-round" on the right part of the pic...here people are inclined with a certain angle with the vertical....as a result cos(theta) component of tension should balance his weight..and a result of it the sin (theta) component provides radial acceleration....
49tut tut!!
here the bead is fixed on the rod!!
so it can no way have an oblique normal reaction!
!!
!!
the string made it have so and thats why in a merry-go-round u do not slide but instead u remain fixed!
but the bead moves radially outward!
so there is a difference certainly! :)
1@subhomoy
am assuming that bead's diameter is more than that of rod...only in this case if the rod rotates its orientation will be oblique ( u can see in the figure i hv made above that i hv taken bead's dia to be more than that of rod).......but if u r considering that bead fits exactly into the rod..i.e they have same radius then u r correct.....normal reaction would not be oblique in that case.....
341Seen from an inertial frame, and choosing an instantaneous axis with \hat {e_{r}} along the radial direction outward and \hat {e_{\theta}} perpendicular to \hat {e_{r}} in the anticlockwise sense, we have the acceleration given by
\vec {a} = \left(\ddot {r} - r (\dot {\theta})^2 \right) \hat {e_{r}} + (2 \dot {r} \dot {\theta} + r \ddot{\theta}) \hat {e_{\theta}}
Look at the - r (\dot {\theta})^2 \hat {e_{r}} term. For the inertial frame observer, this term arises because of the bead's rotation.
Now move to an observer who is on the rotating rod just underneath the bead. From d'Alembert's principle in order that the equations be consistent in this frame, we have to add the term r (\dot {\theta})^2 \hat {e_{r}} as the frame has the acceleration - r (\dot {\theta})^2 \hat {e_{r}} too.
Suppose the bead is tied to a string, this observer would have said that the tension counterbalances this force. However in this case, the observer notes that this force causes the bead to move radially.