1from graph we get eq
a=1-t
now a=d2xdt2
ab karo.
A particle starting frm rest moves in a st. line with acc. as shown in the a - t graph . Find the distance in m travelled by the particle in the first four seconds frm start of its motion.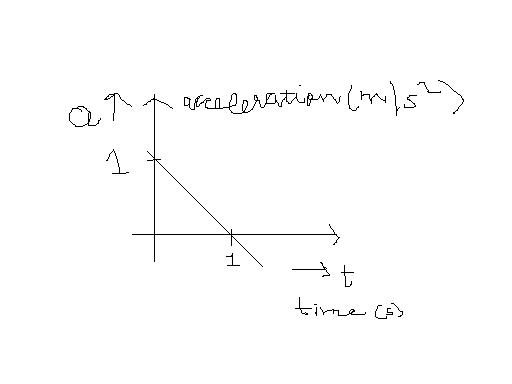
-
UP 0 DOWN 0 0 9
9 Answers
6hmmm..........
so after double integration i get s = t2/2 - t3/6.......
still not gettin the correct ans!!
1observe from graph that eq. of the given line is of form→ y= 1-x
which means that ay=1-ax
ay+ ax =1
dydt + dxdt =1
dy + dx = dt
let dy +dx = dr ( in vector form)
so, dr = dt
now integrating ....
\large \int_{0}^{r}{dr}= \int_{0}^{4}{dt}
which gives r = 4 m.
1@akhil
here distance is asked not displacemnt
here v=t- (t2/2)
so distnce travelled is =∫|v| dt
6hey bornidentity
the particle moves in a st. line
so why r u talkin abt ay and ax????
1above sol. that i posed is wrong.
from graph.
a= 1-t
dvdt=1-t
integrating the above eq. ( 0→v and 0→t ) we get→
v = t - t22 = t(1-t2)
since we need distance we have to take mod of velocity.
v= t(1-t2) , 0≤t≤2
t(t2-1) , 2 ≤t≤4
integrating 1st function within required limit we get, x = 23
similarily integrating 2nd function within required limit we get, x= 103
total distance = 23 + 103 = 4 m