1@ Asish
It is less than 1 hr He is 1 hr early
Car reaches the station in 1 hr . So as he walks some distance ,Car reaches earlier.[23][55]
An engineer works at a plant out of town. A car is sent for him from the plant everyday that arrives at the railway station at the same time as the train on which he comes. One day he arrives at the station one hour before and, without waiting for the car, started walking to work. On his way he met the car and reached the plant 10 minutes before the usual time. How long did the engineer walked before he met the car? Assume all motions with uniform speed.
-
UP 0 DOWN 0 0 41
41 Answers
1
1welllllllllllllllllllllllllll
my next ans is...........
t=(t1-10)/2
where t1=is d usual time
1Let the speed of the person = u
and speed of the car = v
normal time =t
time for which he walked = t1
time he went on car = t2
distance he walked= s1
As the distance is same
s=vt=ut1+vt2
t1+t2= t-10
So, vt= ut1+v[t-10-t1]
t1=(t1+10)v/u
The car could travel s1 in 60-t1 minutes
60-t1=ut1/v
Hence, u/v= (60/t1) -1
Which gives
t1=t1(t1+10)/(60-t1)
60-t1=t1+10
t1=25
ie. the man walks for 25 minutes before getting the car[7][7]
1not necessary asish......let d time travel by car be 20 mins
and d train comes at 5 am..... so d car has to leave by 4.40......
now, train comes at 4 am......d car still starts at 4.40........
but it may meet d man at 4.45.......so d man travels only 45 mins............................
got it asish????? so its not necesary tht it shud be more than an hour
66its neither 15 min, nor 25 min nor more than 1 hr.. why don't you guys try graphical means?
1oh like that question wher 2 guys try to meet in a stipulated time and find their probs of meeting???????
1Now, the man walks for 1 hr before the car arrives at the platform.
that is wrong.......................
he may even get d car earlier 2..... read my explanation daa
106@akand.. the car arrives at the railway station at the same time as the train on which he comes. so if the train arrives at 5am usually the car also arrives at 5 am.. so the day the man reaches the station at 4 am.. the car will arrive at.................................... rite i understood my mistake
1hehe nice explanation asish..............its gud tht u undestood...... now lets solve d question using GRAPHS......................
11Is it 55 mins?
Normal Time = t
St = d
Let
T = Time in walking
y = Time in car
T + y = 1 +t -1/6
Since the man reaches the railway a hour early and he reaches the destination 10mins early.
d = VT +Sy
Now
S(t - 1) = the distance travelled by the car before the man started walking
Therefore
S(t - 1) +VT +ST = d
St + VT +ST = d + S
St +VT +ST = VT + Sy + S
t + T = 1 + y
t + T = 1 + 1 +t - T -1/6
2T = 2 -1/6
T = 1- 1/12
T = 60 - 5
T = 55 mins
Is the asnwer rite sir?
1yes the answer should be 55 mins. one could also do this by assuming time frames.
66Yes, the answer is indeed 55 min.. However, the problem is done most simply (and elegantly) using graphs. For that purpose, take the x-axis running from the station to the factory with the origin being the station. Further, take the origin of time, that is, t = 0, at the ususal time the engineer arrives at the station. Plot the x-vs-t graphs of the car and the engineer. It is as follows: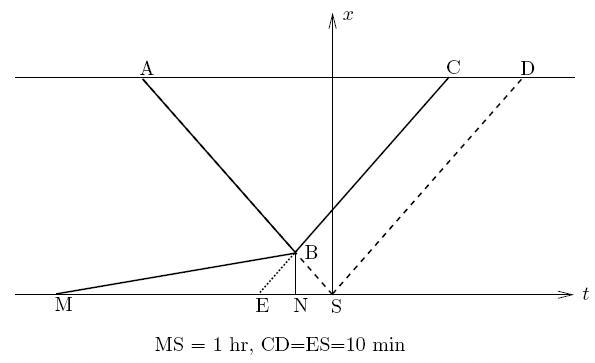
In the diagram attached (not to scale), the broken line ASD represents the usual schedule of the car while ABC is the position vs time graph on that particular day. The segment MB is the position versus time graph for the engineer while he is walking. B is the point where the engineer meets the car.
It is easily seen that triangle EBS is isosceles and EN = SN (here BN is perpendicular to the t-axis). So, SN = ES/2 = CD/2 = 5 min. Accordingly, MN which is the time duration of walking of the engineer is 55 min.
1let d speed of d car be 300 m/mins and d speed of d man be 50m/mins
so according to my ans...
t=50v1/(v2-v1)...........
t=50.50/250
t=10 mins.........
which is fine i guess.....
or v1=300 m/mins and v2=100m/mins
so t=50.100/200
t=25 mins.....
which is also fine i guess
1tooooo many variables and eating my head........already wasted one page hehe
1after doin sum stuff........i got d ans as...
t=(2x-60v1)/(v2-v1)
wher v1= speed of d car
v2= speed of d engineer
and x=distance between d plant and railway station
and 60=60mins..........
1bahut variables consider karna padh raha hai .. i think there is a catch in the question and i am not getting it !
1YIKES..............
now im gettin d ans as.....
t=50v1/(v2-v1)...........
50=50 mins........
sir is this correct??
1gr8 answer ! kya boss abhi tak mere se gussa hai ... i was drunk yaar !
1nahi rey...................this question is gr8 naa?????
wel d ans is
t=50v1/(v2-v1)...........
v1 and v2 in metr/mins.........