can no one help ??
The horizontal bottom of a wide vessel with an ideal fluid has a round orifice of radius R1 over which a round closed cylinder is mounted, whose radius R2>R1( see the figure ) . The clearance between the cylinder and the bottom of the vessel is very small, the fluid density is \rho . find the static pressure of the fluid in the clearance as a function of the distance ' r ' from the axis of the orifice( and the cylinder ),if the height of the fluid is equal to ' h '
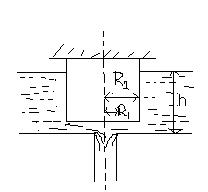
-
UP 0 DOWN 0 0 6

6 Answers
tis frm irodov innit??
let h be height of clearance
at any radius r
so eq of continuity we ger
2\pi R_{1}hv_{1}= 2\pi rhv= 2\pi R_{2}hv_{2}
so R_{1}v_{1}= rv= R_{2}v_{2}
also v_{1}= \sqrt{2gh}
also P+1/2\rho v^{2}=P_{0}+1/2\rho v_{1}^{2}
so P=P_{0}+1/2\rho v_{1}^{2}\left(1-\left(v/v_{1} \right)^{2} \right)
put v_{1}= \sqrt{2gh}
and v/v_{1}=R_{1}/r
please can u use latex ur symbol's are confusing. Unable to understand.
brother check this post to make ur latex work....http://www.targetiit.com/iit-jee-forum/posts/latex-not-workin-15025.html