A rod of length 10 m. is travelling on a smooth,level,horizontal surface.Beyond a point A,the floor ceases to be smooth and the coefficient of friction is k=0.1.The rod is travelling such that it is moving towards the point A.The front end of the rod crosses the point A at t=0 with velocity v.If at t=T, the rod stops then find T. Assume that the rough patch is sufficiently long.
-
UP 0 DOWN 0 1 2
2 Answers
1161Check whether the answer is: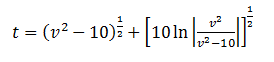 
Sushovan Halder Sir actually the answer is given to the nearest integer which is 5s.
Upvote·0· Reply ·2014-06-17 09:37:19- Akash Anand You have not provided v, if you have value for v then put it and try to find out the result. I am sure you will get it. I will post the solution, once you confirm it.
263SIR,no value of v has been given.The solution posted was like this:
The friction is varying and depends on the mass of the rod on the rough surface.Let the rod travel by a distance x.
So the normal force on the rod due to the rough surface,N=λxg................(1),where λ is mass per unit length.We have considered only the normal force exerted by the rough surface because friction is provided by this rough surface only.As there is relative slipping along the ground so the friction is at it's maximum value.So fmax=kλxg.....(2)
So, m*a=-kλxg......[a is the accleration]
or, a=-kλxg/m
or, a=-kxg/l....................[As m=λ*l]
or, a + (kg/l)*x=0.............(3)
Now this is the standard differential equation which we have read in S.H.M.
The solution to this equation is x=Asin(w*t + φ)
where w=√(kg/l).
At t=0 x=0,
so sinφ=0
or, φ=0.
So the equation reduces to x=Asin(w*t).
Differentiating this equation w.r.t time we get
v=Awcos(w*t).
We have to find when the velocity of this rod becomes 0,
so v=0
or, Awcos(w*t)=0
or, wt=Ï€/2......................(4)
or, t=Ï€/(2w)=(Ï€/2)*√(l/kg)=5s nearly.
NOTE:There are infinite solutions to equation (4). So we have to consider the time when the rod's velocity first becomes 0.Obviously after v=0 the rod will not move,but since we have used the equations of S.H.M. so WITH RESPECT TO THIS EQUATION WE NEED TO FIND OUT WHEN THE ROD'S VELOCITY FIRST BECOMES 0.
- Akash Anand This explanation is good enough, but i have done with different approach and i guess from that also you will get the answer.
- Akash Anand Just think a while, friction is independent of rod's initial speed. So if the speed will be higher, then obviously it will take larger time to stop it. The solution given here is a different way to look this question altogether.