1calculation part left for u[3][3]
I hope i'm rite with my aaproach
(1)
2 loudspeakers are emitting sound waves of wavelength \lambda with an initial phase difference of \frac{\Pi }{2}.At what minimum distance from O on line AB will one hear a maxima?
(A)25\lambda (B)\frac{100\lambda }{\sqrt{15}}
(C)\frac{25\lambda }{3} (D)50\lambda
(2)
Two long straight wires of telephone circuit inside a house are coplanar with and run parallel to a third long straight conductor that carries a current i = i0 sin\omega t. The wires are at a distance of d1 and d2 from the conductor. The conductor induced a noise in the telephone circuit. What is the rms voltage per unit length of this induced emf ? Express your answer in \mu V.
Given that d_{2}=2d_{1}, i_{0}=\frac{2\sqrt{2}}{\ln 2}A\omega =50 rad/sec.
-
UP 0 DOWN 0 0 8
8 Answers
11) 
yaar I tried as this : got heavy amount of calculations though...
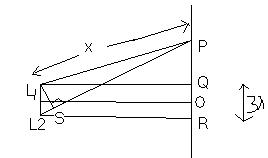
In abv fig. L2P - L1P = Path difference = Δx
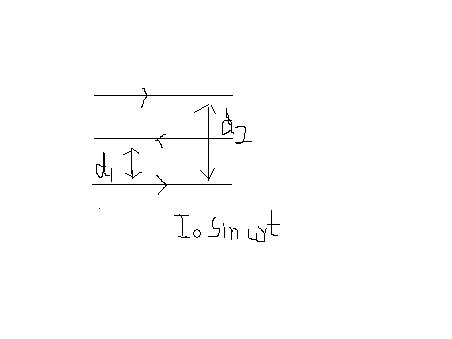
let y1 = A sin ωt
and y 2 = A sin (ωt + π2 ) as mentioned that phase diff. is π2
now Let y is the resulting wave due to interference
y = y1+y2
= A{ sin ωt + sin (ωt + π2 ) }
= 2A sin (ωt + π4) cos (-π4) [ using sinc+ sinD = 2 sin C+D2cosC-D2 ]
= √2 A sin (ωt + Ï€4)
we have δ = π4 ......................(1)
also according to formula we have δ = 2πλΔx = π4 from (1)
now we got Δx = λ8
we got path difference is equal to λ8
so according to the figure (L2P)2 = PR 2 + L2R 2
(L2P)2 = (PQ + QR) 2 + L2R 2............(2)
we know QR and we need to find out PQ
we also have L1P2 = L1Q2+PQ2 → PQ2=x2-(100λ)2................(3)
we subsitute the value of PQ2 from (3) in (2) to find out x and finall y substitute x in (3) to get PQ which is asked in the question
11I hav tried like dis and got d answer.
\bigtriangleup \phi =2n\Pi
\Rightarrow \frac{\Pi }{2}+\frac{2\Pi }{\lambda }d sin\theta=2n\Pi
\frac{2\Pi }{\lambda }d sin\theta =(2n-\frac{1}{2})\Pi
\Rightarrow sin\theta =(2n-\frac{1}{2})\frac{\lambda }{2d}=\frac{1}{2}\times \frac{\lambda }{2\times 3\lambda }=\frac{1}{12}
\Rightarrow \frac{y}{\sqrt{(100\lambda )^{2}}}=\frac{1}{12}
\Rightarrow 144y^{2}=(100\lambda)^{2}
\Rightarrow y=\frac{100\lambda }{12}=\frac{25\lambda}{3}
1No d correct answer is c.I did it after thinking 5 days but not sure about d process.If dis process is correct, Can i apply this 2 other similar problems???
1if u got the answer it's ok.........par tera method mujhe jyada samajh nahin aaya..
66The basic idea is the following:
When two monochromatic coherent waves superimpose at a point, the resulting intensity will depend on the (constant) phase difference between them. The resultant intensity will be greatest if the phase difference is an even multiple of pi, and minimum if the phase difference is an odd multiple of pi.
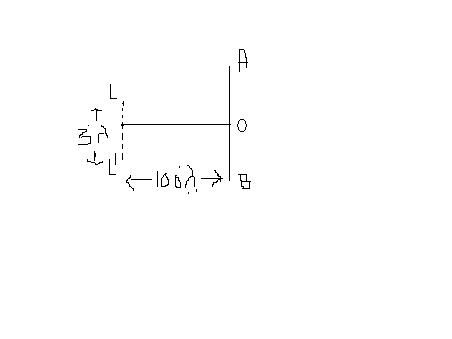
For the present case, at any point P on AB such that the line joining the center of LL' and P makes an angle θ with the horizontal, the two waves come with a path difference = LL' sin θ = d sin θ, where I have taken the distance LL' = d.
The corresponding phase difference arising due to this path = 2πλ d sin θ. There is an additional phase difference of π/2 at the sources themselves. This makes the total phase difference at the point P as
2πλ d sin θ + π2
Next, since the distance between the source plane and AB is 100λ which is much greater than 3λ, we may safely write down sin θ = tan θ = yD where D = 100λ and y is the position relative to O (+ve being taken upward).
Accordingly the total phase difference at P takes the form
2πλ d yD + π2 = 2πλ 3 y100 + π2
For maximum, this phase difference must equal 2kπ for some integer k.
This gives,
y = \left(2k-\dfrac{1}{2}\right)\dfrac{50}{3}\lambda
Its easy to see that this is least for k = 0, whence
y = -\dfrac{25}{3}\lambda
the negative sign indicating that the point P will be below O and its distance from O is just the modulus of the above value of y.