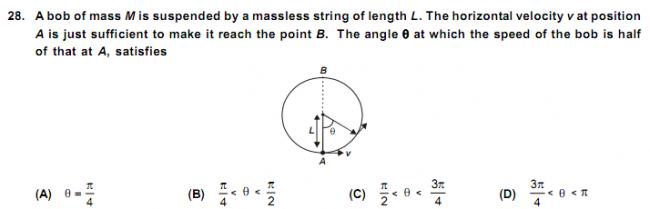
71Answer given is correct.. I got θ ≈ 150°
Resolve it.. may be you'' get it. Somewhere silly mistake you might have done.
Btw, How much are you expecting in 12th Feb's test.. Seeing your past performance , I'm presuming around ≈ 290 for you .. :)
I had a request.. Since you have a scanner at hand, could you upload one or more papers of RTPF.. these are completely inaccessible to me.
71I take θ from the vertical.
So we have, By energy Conservation,
=> mV2 = 2mgl(1+cos θ) + mV24
=> 3mV24 = 2mgl(1+cos θ)
V2 = 5gl
Putting, cos θ = 7/8 ≈ 28.96°
So, α = Π- θ = 180° - 28.96° = 151.04° > 3Π4
262@vivek - it is given that velocity imparted is such that the particle just reaches B (not that it completes the circular motion) .
so shouldnt it be v2=4gl ??
71It means that the string just on the verge of becoming slack at the topmost point... It however successfully completes the HALF CIRCLE... However it it was what you said, the string would slack at during time before going to top..
[ You didn't answer my hided post. Please answer ]
7If the velocity that aditya mentioned was imparted then the the bob wud undergo projectile motion since tension wud becum 0 (not velocity).and it wud reach a height upto 50L/27.
21Interesting observation.
When θ<90
velocity becomes 0 before tension does.
when θ=90
Velocity and tension become zero at the same time.
When θ>90
tension becomes 0 before velocity does.
