3sir but how u get the direction for friction
A uniform disc of mass m and radius r is rolling on a circle by virtue of torque Ï„ given to rod(mass M length L) pivoted to disc.Find angular accelrations of rod and disc.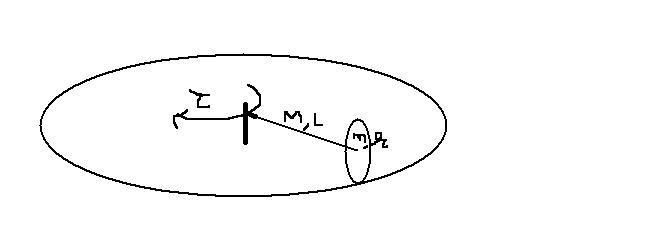
-
UP 0 DOWN 0 0 47
47 Answers
1bhiyya in my eqn α is ang. acc. of the rod
so the ang acc. of disc should be αL/r ??[7]
in 2nd eq is for c.o.m of disc the force due to (tau) is doubtful
maybe i have messed it up completely plz help...[2]
62oh sorry din read properly... u are right...
I have the feeling that ur equation is correct
I will also get confused if ur equaton is not correct!!
1no there shud be something wrong
see we can get α very easily using only two of the three eqns
this is weird.. isn't it.
but one thing is sure from eurekas ans that αdisc=αL/r
and plz dont get confused
3ok wats the direction of the friction sir.for pure rolling wont it be static friction
1ok someone told me this was gyroscopic motion and is not in course
pirate (abhishek) has already shouted that on one of the first posts
if this is so im not going to waste more time on it
62@sankara yup there will be only static friction that is why we have used F and not k.N
@Philip:
(tau) - FL= Iα (1)
(tau)/L - F = ma where a =αL (2)
Fr =(mr2/2)a/r (3)
there are 3 variables.. F, a , α
What is wrong with having 3 equations! :O
1arre bhaiyya aise toh a =αL bhi ek eqn hai
P.S. sorry for that four in a row it was not your optical illusion it was some network fault [3]
62(tau) - FL= Iα (1)
(tau)/L - F = ma
a =αL (2)
are essentially two equations only!! :O
The 2nd is division of the first by L!
62hint for direction:
first solve when there is no friction....
Friction oppsoes the motion
3philip there will be no torque tau that is due to the external torque abt the central axis
62arrey first just find the direction in which the surfaces will move when there is no friction acting....
Now try to see that friction will only prevent this slight relative motion..
1bhaiya either im blind or in need of good sleep
you said: -
(tau) - FL= Iα (1)
(tau)/L - F = ma
a =αL (2)
are essentially two equations only!! :O
The 2nd is division of the first by L!
now please clarify how is this "2nd is division of the first by L!"
in (1) there is 'I' which is very numerically and (i think dimensionnally too) different from 'm' i know i can bore you by repeating this but i
really think i've messed it up
62@philip.. did i misread it again....
These to me are the 3 equation...
(Torque does not contribute to the force equation.. that is why your secodn equation is not true!!!
(tau) - FL= Iα (1)
a =αL (2)
Fr =(mr2/2)a/r (3)
thus, FL =(mr2/2)αL2/r2
substitute in 1
(tau) - (mr2/2)αL2/r2 = I α
(tau) = { mL2/2 + I } α
I = ML2/3 + m22/4+mL2
To me, this should give the answer... i know it is probably not matching eureka's...
so i am making a blunder that is unwarrented.. and not acceptable :(
1how tau doesnt contribute to the force [7]
roughly ...... if there is no friction the c.o.m of disc will still be accelerating??
in presence of no force ???
or the effect is sort of compensated in calculation of α??
62yeah essentially we dont consider torques to cause any acceleration fo the linear kind..
they only cause angular accelerations..
So by doing this u are double counting the effect of the torque!
33inertia along the center will be ML2/3 + mr2/4+mL2
i was just taking this wrong...
I took ML2/3 + mL2 only.. [3]
33not a wastage of time...
everything u do pays u in long run [1]
62it is very much in the syllabus..
It is good that we discussed this ... cos u need to understand that torques cause only rotation.. no linear motion1
33Sorry!:(
no idea..
the problems in which the axis of rotation of a body is also rotating is not in the syllabus i think..
But will be happy to see a soln.. [2] [1]
33But i got something :(
tell me if its the answer..
ang acc of disc= 3Ï„
Lr(M+3m)
33Then i hopeless in this :(
plz post teh answrer atleat so that can think of how to get it [3][3]