If all the particles of a system lie in a cube,is it necessary that the CM be in the cube ??
I thinks the ans shud b NO.
106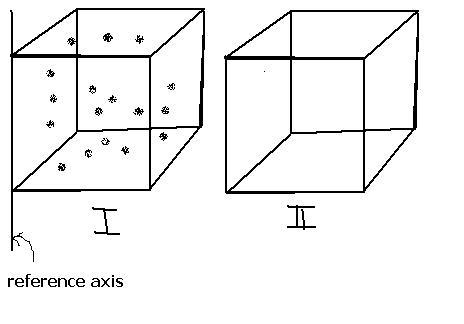
Consider cube I:
Let there be n-particles.(all are identical for simplicity)
Let the position (r) of ith particle be ri
So, the COM = (Σmri)/nm
= Σri/n
Now, Σri is maximum when each ri = max = a (side of cube) ... (I am just calculating x-coordinate)
So, Σri max = na
So, RCOM max = na/n = a
So, the max value of x-coordinate of COM = a i.e. on the cube
9its obvious the ans is yes how are u saying No pls provide ur argument
proof
frm CM Σmr =0
now if its outside cube , all the r vectors are torwards the cube and hence their summation cant be 0 . (as the net vector is always pointing towards cube and cant be null )
24Yes, for symmetrical and uniform bodies, the COM is the geometrical centre of the body which for a cube lies inside it. Even if the mass distribution is not uniform, the com would lie somewhere inside the cube only because the mass is inside the cube only.
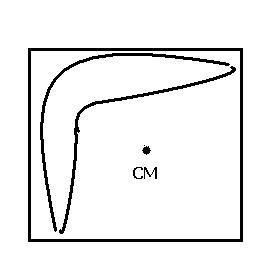
11I was thinking in this way-- what if the particles of the system were arranged in the shape of a boomerang like in the fig... After all its completely r freedom to chose the system of particles.. then as we can c the CM goes out of the cube.
11@Celestine - this is how i was considering and that is y i thought it is not always necessary
106how does the CM go outside the cube here? It is inside isnt it?
24Copied from net..
A center of mass (CM) of a boomerang, depending upon its particular shape and design, is not located on the device, itself. If you orient the boomerang so that it appears to form the letter V, its CM will be located directly over the vertex. The distance above the vertex will vary depending upon the boomerang's design. When you toss the boomerang, it will spin about its CM.
You may be able to determine a boomerang's CM by doing the following: Suspend the device from a string. The CM will align with the string. Since the CM is also located directly above the vertex, the intersection of the line bisecting the vertex and the line extending downward from the string should locate the CM.
So clearly in ur question,,,CM will lie inside the cube
11ok then it will b inside.. r u sure ??i thought it would b in the same pos but above the boomerang ??
