1:-)
A massive vertical wall is approaching a man at a speed u. When it is at a distance of 10 m, the man throws a ball with speed 10 m/s at an angle of 37° which after completely elastic rebound reaches back directly into his hands. find the velocity u of the wall.
1. 10/3 m/s
2. 15/3 m/s
3. 13/3 m/s
4. none
-
UP 0 DOWN 0 0 17
17 Answers
21@aveek thadey ko ek mahiney baad yaad aayi iski......[3]
lmao
1So the answer is 25/3 indeed . Now someone say that my REASONING WAS WRONG ......... ?????
21
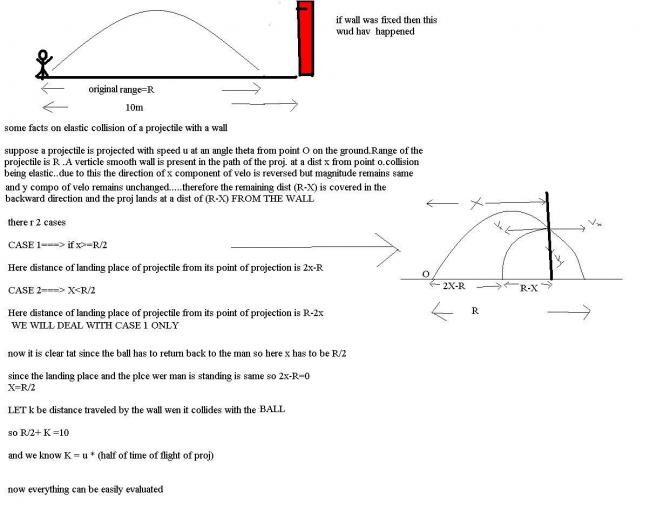
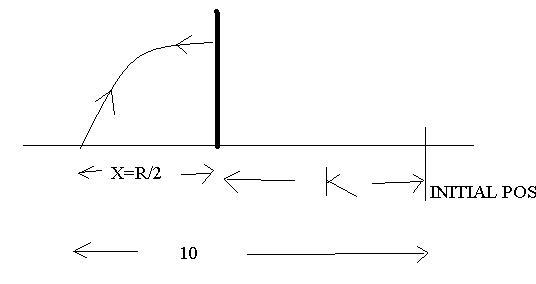
here we hav taken half of time of flight of the proj bec wen proj has travelled R/2 DIST IN HORIZONTAL then it is at its max height.....and time taken by ball to reach max height is half of time of flight
1see this is the working which i hv worked out
the horizontal component of vel is 8 and le tthe vel of the wall be u
therefrore time taken for collision is 10/8+u (sinple rel motion concept0
now
during this time distance covered by the ball is 8*(10/8+u)=80/10+u
nw after collision its vertical component of vel will remain unchanged and its horizonatal component will beomce 8+u
since the ball again reaches the man thereofre the smae distance will be covered or again the distance covered will be 80/10+u
therefore the time taken to complete this will be......
80/10+u)/8+u
since 8+u is the new vel
this is for the horizonatal motion
now for the vertical component
at the time of collision the vertical distance will be covered y
and the vel on the y direction can be easily found out
now after time t vel in y direction will remain constant and now
since it reaches the same pnt
vertical distance covered in the y axis will be
-y
or
-y=ut-5t^2
where t is the time which we calculated and u os the vel before collision
1@Anirudh....the ball finally comes back to the man......when the wall has moved a dist. in time t secs. the ball hits it perpendicularly at that instant...otherwise how can it finally reach the man after elastic collision ? It'd have jumped to some other angle....what do u say abt. it ??
1Aveek here at the time of collision the velocities of the ball w.r.t to ground won't be horizontal . it will have some vertical component .
thus your reasoning is wrong.
1The ball can come back directly into the hands only if it hits the wall perpendicularly with elastic collision.
hence vx of the ball = v cos θ . t = 8t
rel vel of approach of ball and wall = (8t+u)
hence time of meeting = 108t+u
and vy of the ball is 0 as it hits the wall perpendicularly.
v sinθ - gt = 0
or 6 = gt
or t = 6g
hence 108t+u = 6g
taking g as 9.8
we get u = 25/3 .....hence none
someone please verify it.
